
An acid is a molecule or ion capable of either donating a proton (i.e. hydrogen ion, H+), known as a Brønsted–Lowry acid, or forming a covalent bond with an electron pair, known as a Lewis acid.

In chemistry, an acid–base reaction is a chemical reaction that occurs between an acid and a base. It can be used to determine pH via titration. Several theoretical frameworks provide alternative conceptions of the reaction mechanisms and their application in solving related problems; these are called the acid–base theories, for example, Brønsted–Lowry acid–base theory.

In chemistry, a hydrogen bond is primarily an electrostatic force of attraction between a hydrogen (H) atom which is covalently bonded to a more electronegative "donor" atom or group (Dn), and another electronegative atom bearing a lone pair of electrons—the hydrogen bond acceptor (Ac). Such an interacting system is generally denoted Dn−H···Ac, where the solid line denotes a polar covalent bond, and the dotted or dashed line indicates the hydrogen bond. The most frequent donor and acceptor atoms are the period 2 elements nitrogen (N), oxygen (O), and fluorine (F).

In the Arrhenius model of reaction rates, activation energy is the minimum amount of energy that must be available to reactants for a chemical reaction to occur. The activation energy (Ea) of a reaction is measured in kilojoules per mole (kJ/mol) or kilocalories per mole (kcal/mol). Activation energy can be thought of as the magnitude of the potential barrier (sometimes called the energy barrier) separating minima of the potential energy surface pertaining to the initial and final thermodynamic state. For a chemical reaction to proceed at a reasonable rate, the temperature of the system should be high enough such that there exists an appreciable number of molecules with translational energy equal to or greater than the activation energy. The term "activation energy" was introduced in 1889 by the Swedish scientist Svante Arrhenius.

A Lewis acid (named for the American physical chemist Gilbert N. Lewis) is a chemical species that contains an empty orbital which is capable of accepting an electron pair from a Lewis base to form a Lewis adduct. A Lewis base, then, is any species that has a filled orbital containing an electron pair which is not involved in bonding but may form a dative bond with a Lewis acid to form a Lewis adduct. For example, NH3 is a Lewis base, because it can donate its lone pair of electrons. Trimethylborane () is a Lewis acid as it is capable of accepting a lone pair. In a Lewis adduct, the Lewis acid and base share an electron pair furnished by the Lewis base, forming a dative bond. In the context of a specific chemical reaction between NH3 and Me3B, a lone pair from NH3 will form a dative bond with the empty orbital of Me3B to form an adduct NH3•BMe3. The terminology refers to the contributions of Gilbert N. Lewis.
HSAB is an acronym for "hard and soft (Lewis) acids and bases". HSAB is widely used in chemistry for explaining the stability of compounds, reaction mechanisms and pathways. It assigns the terms 'hard' or 'soft', and 'acid' or 'base' to chemical species. 'Hard' applies to species which are small, have high charge states, and are weakly polarizable. 'Soft' applies to species which are big, have low charge states and are strongly polarizable.

In chemistry, charge-transfer (CT) complex, or electron donor-acceptor complex, describes a type of supramolecular assembly of two or more molecules or ions. The assembly consists of two molecules that self-attract through electrostatic forces, i.e., one has at least partial negative charge and the partner has partial positive charge, referred to respectively as the electron acceptor and electron donor. In some cases, the degree of charge transfer is "complete", such that the CT complex can be classified as a salt. In other cases, the charge-transfer association is weak, and the interaction can be disrupted easily by polar solvents.
The bond-dissociation energy is one measure of the strength of a chemical bond A−B. It can be defined as the standard enthalpy change when A−B is cleaved by homolysis to give fragments A and B, which are usually radical species. The enthalpy change is temperature-dependent, and the bond-dissociation energy is often defined to be the enthalpy change of the homolysis at 0 K, although the enthalpy change at 298 K is also a frequently encountered parameter.
Dimethylformamide is an organic compound with the chemical formula HCON(CH3)2. Its structure is HC(=O)−N(−CH3)2. Commonly abbreviated as DMF, this colourless liquid is miscible with water and the majority of organic liquids. DMF is a common solvent for chemical reactions. Dimethylformamide is odorless, but technical-grade or degraded samples often have a fishy smell due to impurity of dimethylamine. Dimethylamine degradation impurities can be removed by sparging samples with an inert gas such as argon or by sonicating the samples under reduced pressure. As its name indicates, it is structurally related to formamide, having two methyl groups in the place of the two hydrogens. DMF is a polar (hydrophilic) aprotic solvent with a high boiling point. It facilitates reactions that follow polar mechanisms, such as SN2 reactions.

In coordination chemistry, metal ammine complexes are metal complexes containing at least one ammonia ligand. "Ammine" is spelled this way for historical reasons; in contrast, alkyl or aryl bearing ligands are spelt with a single "m". Almost all metal ions bind ammonia as a ligand, but the most prevalent examples of ammine complexes are for Cr(III), Co(III), Ni(II), Cu(II) as well as several platinum group metals.
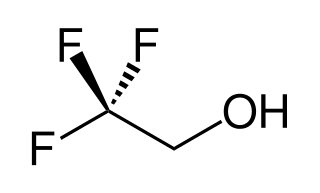
2,2,2-Trifluoroethanol is the organic compound with the formula CF3CH2OH. Also known as TFE or trifluoroethyl alcohol, this colourless, water-miscible liquid has a smell reminiscent of ethanol. Due to the electronegativity of the trifluoromethyl group, this alcohol exhibits a stronger acidic character compared to ethanol.
In chemistry a donor number (DN) is a quantitative measure of Lewis basicity. A donor number is defined as the negative enthalpy value for the 1:1 adduct formation between a Lewis base and the standard Lewis acid SbCl5 (antimony pentachloride), in dilute solution in the noncoordinating solvent 1,2-dichloroethane with a zero DN. The units are kilocalories per mole for historical reasons. The donor number is a measure of the ability of a solvent to solvate cations and Lewis acids. The method was developed by V. Gutmann in 1976. Likewise Lewis acids are characterized by acceptor numbers (AN, see Gutmann–Beckett method).

In chemistry, an adduct is a product of a direct addition of two or more distinct molecules, resulting in a single reaction product containing all atoms of all components. The resultant is considered a distinct molecular species. Examples include the addition of sodium bisulfite to an aldehyde to give a sulfonate. It can be considered as a single product resulting from the direct combination of different molecules which comprises all atoms of the reactant molecules.

Antimony pentachloride is a chemical compound with the formula SbCl5. It is a colourless oil, but typical samples are yellowish due to dissolved chlorine. Owing to its tendency to hydrolyse to hydrochloric acid, SbCl5 is a highly corrosive substance and must be stored in glass or PTFE containers.

In chemistry, transition state theory (TST) explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.

Diethyl sulfide is an organosulfur compound with the chemical formula (CH3CH2)2S. It is a colorless, malodorous liquid. Although a common thioether, it has few applications.
In coordination chemistry, a stability constant is an equilibrium constant for the formation of a complex in solution. It is a measure of the strength of the interaction between the reagents that come together to form the complex. There are two main kinds of complex: compounds formed by the interaction of a metal ion with a ligand and supramolecular complexes, such as host–guest complexes and complexes of anions. The stability constant(s) provide(s) the information required to calculate the concentration(s) of the complex(es) in solution. There are many areas of application in chemistry, biology and medicine.
Acid strength is the tendency of an acid, symbolised by the chemical formula , to dissociate into a proton, , and an anion, . The dissociation or ionization of a strong acid in solution is effectively complete, except in its most concentrated solutions.
In chemistry, the Gutmann–Beckett method is an experimental procedure used by chemists to assess the Lewis acidity of molecular species. Triethylphosphine oxide is used as a probe molecule and systems are evaluated by 31P-NMR spectroscopy. In 1975, Viktor Gutmann used 31P-NMR spectroscopy to parameterize Lewis acidity of solvents by acceptor numbers (AN). In 1996, Michael A. Beckett recognised its more generally utility and adapted the procedure so that it could be easily applied to molecular species, when dissolved in weakly Lewis acidic solvents. The term Gutmann–Beckett method was first used in chemical literature in 2007.

Rhodium carbonyl chloride is an organorhodium compound with the formula Rh2Cl2(CO)4. It is a red-brown volatile solid that is soluble in nonpolar organic solvents. It is a precursor to other rhodium carbonyl complexes, some of which are useful in homogeneous catalysis.
















