List of regular polytope compounds

Last updated

This article lists the regular polytope compounds in Euclidean, spherical and hyperbolic spaces.

Contents

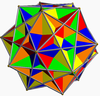
Two dimensional compounds

For any natural number n, there are n-pointed star regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n−m)}) and m and n are coprime. When m and n are not coprime, the star polygon obtained will be a regular polygon with n/m sides. A new figure is obtained by rotating these regular n/m-gons one vertex to the left on the original polygon until the number of vertices rotated equals n/m minus one, and combining these figures. An extreme case of this is where n/m is 2, producing a figure consisting of n/2 straight line segments; this is called a degenerate star polygon.

In other cases where n and m have a common factor, a star polygon for a lower n is obtained, and rotated versions can be combined. These figures are called star figures, improper star polygons or compound polygons. The same notation {n/m} is often used for them, although authorities such as Grünbaum (1994) regard (with some justification) the form k{n} as being more correct, where usually k = m.

A further complication comes when we compound two or more star polygons, as for example two pentagrams, differing by a rotation of 36°, inscribed in a decagon. This is correctly written in the form k{n/m}, as 2{5/2}, rather than the commonly used {10/4}.

Coxeter's extended notation for compounds is of the form c{m,n,...}[d{p,q,...}]e{s,t,...}, indicating that d distinct {p,q,...}'s together cover the vertices of {m,n,...} c times and the facets of {s,t,...} e times. If no regular {m,n,...} exists, the first part of the notation is removed, leaving [d{p,q,...}]e{s,t,...}; the opposite holds if no regular {s,t,...} exists. The dual of c{m,n,...}[d{p,q,...}]e{s,t,...} is e{t,s,...}[d{q,p,...}]c{n,m,...}. If c or e are 1, they may be omitted. For compound polygons, this notation reduces to {nk}[k{n/m}]{nk}: for example, the hexagram may be written thus as {6}[2{3}]{6}.

Examples for n=2..10, nk≤30
Regular star figure 2(2,1).svg
2{2}		 Regular star figure 3(2,1).svg
3{2}		 Regular star figure 4(2,1).svg
4{2}		 Regular star figure 5(2,1).svg
5{2}		 Regular star figure 6(2,1).svg
6{2}		 Regular star figure 7(2,1).svg
7{2}		 Regular star figure 8(2,1).svg
8{2}		 Regular star figure 9(2,1).svg
9{2}		 Regular star figure 10(2,1).svg
10{2}		 Regular star figure 11(2,1).svg
11{2}		 Regular star figure 12(2,1).svg
12{2}		 Regular star figure 13(2,1).svg
13{2}		 Regular star figure 14(2,1).svg
14{2}		 Regular star figure 15(2,1).svg
15{2}
Regular star figure 2(3,1).svg
2{3} 		Regular star figure 3(3,1).svg
3{3} 		Regular star figure 4(3,1).svg
4{3} 		Regular star figure 5(3,1).svg
5{3} 		Regular star figure 6(3,1).svg
6{3} 		Regular star figure 7(3,1).svg
7{3}		 Regular star figure 8(3,1).svg
8{3}		 Regular star figure 9(3,1).svg
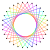9{3}		 Regular star figure 10(3,1).svg
10{3}		 Regular star figure 2(4,1).svg
2{4} 		Regular star figure 3(4,1).svg
3{4} 		Regular star figure 4(4,1).svg
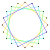4{4} 		Regular star figure 5(4,1).svg
5{4} 		Regular star figure 6(4,1).svg
6{4}		 Regular star figure 7(4,1).svg
7{4}
Regular star figure 2(5,1).svg
2{5} 		Regular star figure 3(5,1).svg
3{5} 		Regular star figure 4(5,1).svg
4{5} 		Regular star figure 5(5,1).svg
5{5}		 Regular star figure 6(5,1).svg
6{5}		 Regular star figure 2(5,2).svg
2{5/2}		 Regular star figure 3(5,2).svg
3{5/2}		 Regular star figure 4(5,2).svg
4{5/2}		 Regular star figure 5(5,2).svg
5{5/2}		 Regular star figure 6(5,2).svg
6{5/2}		 Regular star figure 2(6,1).svg
2{6} 		Regular star figure 3(6,1).svg
3{6} 		Regular star figure 4(6,1).svg
4{6}		 Regular star figure 5(6,1).svg
5{6}
Regular star figure 2(7,1).svg
2{7} 		Regular star figure 3(7,1).svg
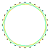3{7}		 Regular star figure 4(7,1).svg
4{7}		 Regular star figure 2(7,2).svg
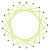2{7/2}		 Regular star figure 3(7,2).svg
3{7/2}		 Regular star figure 4(7,2).svg
4{7/2}		 Regular star figure 2(7,3).svg
2{7/3}		 Regular star figure 3(7,3).svg
3{7/3}		 Regular star figure 4(7,3).svg
4{7/3}		 Regular star figure 2(8,1).svg
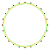2{8} 		Regular star figure 3(8,1).svg
3{8}		 Regular star figure 2(8,3).svg
2{8/3}		 Regular star figure 3(8,3).svg
3{8/3}
Regular star figure 2(9,1).svg
2{9} 		Regular star figure 3(9,1).svg
3{9}		 Regular star figure 2(9,2).svg
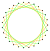2{9/2}		 Regular star figure 3(9,2).svg
3{9/2}		 Regular star figure 2(9,4).svg
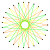2{9/4}		 Regular star figure 3(9,4).svg
3{9/4}		 Regular star figure 2(10,1).svg
2{10} 		Regular star figure 3(10,1).svg
3{10}		 Regular star figure 2(10,3).svg
2{10/3}		 Regular star figure 3(10,3).svg
3{10/3}
Regular star figure 2(11,1).svg
2{11}		 Regular star figure 2(11,2).svg
2{11/2}		 Regular star figure 2(11,3).svg
2{11/3}		 Regular star figure 2(11,4).svg
2{11/4}		 Regular star figure 2(11,5).svg
2{11/5}		 Regular star figure 2(12,1).svg
2{12} 		Regular star figure 2(12,5).svg
2{12/5}		 Regular star figure 2(13,1).svg
2{13}		 Regular star figure 2(13,2).svg
2{13/2}		 Regular star figure 2(13,3).svg
2{13/3}		 Regular star figure 2(13,4).svg
2{13/4}		 Regular star figure 2(13,5).svg
2{13/5}		 Regular star figure 2(13,6).svg
2{13/6}
Regular star figure 2(14,1).svg
2{14}		 Regular star figure 2(14,3).svg
2{14/3}		 Regular star figure 2(14,5).svg
2{14/5}		 Regular star figure 2(15,1).svg
2{15} 		Regular star figure 2(15,2).svg
2{15/2}		 Regular star figure 2(15,4).svg
2{15/4}		 Regular star figure 2(15,7).svg
2{15/7}

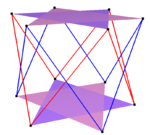
Regular skew polygons also create compounds, seen in the edges of prismatic compound of antiprisms, for instance:

Regular compound skew polygon
Compound
skew squares		Compound
skew hexagons		Compound
skew decagons
Two {2}#{ }Three {2}#{ }Two {3}#{ }Two {5/3}#{ }
Compound skew square in cube.png Skew tetragons in compound of three digonal antiprisms.png Compound skew hexagon in hexagonal prism.png Compound skew hexagon in pentagonal crossed antiprism.png

Three dimensional compounds

A regular polyhedron compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. With this definition there are 5 regular compounds.

Symmetry[4,3], Oh[5,3]+, I[5,3], Ih
DualitySelf-dualDual pairs
Image Compound of two tetrahedra.png Compound of five tetrahedra.png Compound of ten tetrahedra.png Compound of five cubes.png Compound of five octahedra.png
Spherical Spherical compound of two tetrahedra.png Spherical compound of five tetrahedra.png Spherical compound of ten tetrahedra.png Spherical compound of five cubes.png Spherical compound of five octahedra.png
Polyhedra 2 {3,3} 5 {3,3} 10 {3,3} 5 {4,3} 5 {3,4}
Coxeter {4,3}[2{3,3}]{3,4} {5,3}[5{3,3}]{3,5} 2{5,3}[10{3,3}]2{3,5} 2{5,3}[5{4,3}][5{3,4}]2{3,5}

Coxeter's notation for regular compounds is given in the table above, incorporating Schläfli symbols. The material inside the square brackets, [d{p,q}], denotes the components of the compound: d separate {p,q}'s. The material before the square brackets denotes the vertex arrangement of the compound: c{m,n}[d{p,q}] is a compound of d {p,q}'s sharing the vertices of an {m,n} counted c times. The material after the square brackets denotes the facet arrangement of the compound: [d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the faces of {s,t} counted e times. These may be combined: thus c{m,n}[d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the vertices of {m,n} counted c times and the faces of {s,t} counted e times. This notation can be generalised to compounds in any number of dimensions. [1]

If improper regular polyhedra (dihedra and hosohedra) are allowed, then two more compounds are possible: 2{3,4}[3{4,2}]{4,3} and its dual {3,4}[3{2,4}]2{4,3}. [2]

Euclidean and hyperbolic plane compounds

There are eighteen two-parameter families of regular compound tessellations of the Euclidean plane. In the hyperbolic plane, five one-parameter families and seventeen isolated cases are known, but the completeness of this listing has not yet been proven. [2]

Euclidean regular compounds [2]
TessellationsCondition
Self-dual
{4,4}[(b2+c2){4,4}]{4,4}b ≥ c ≥ 0, b > 0
2{4,4}[2(b2+c2){4,4}]2{4,4}bc(b − c) > 0
Dual pairs
{3,6}[(b2+bc+c2){3,6}]2{6,3}2{3,6}[(b2+bc+c2){6,3}]{6,3}b ≡ c mod 3
2{3,6}[2(b2+bc+c2){3,6}]4{6,3}4{3,6}[2(b2+bc+c2){6,3}]2{6,3}b ≡ c mod 3, bc(b − c) > 0
{6,3}[2(b2+bc+c2){3,6}]2{3,6}2{6,3}[2(b2+bc+c2){6,3}]{3,6}b ≡ c mod 3
2{6,3}[4(b2+bc+c2){3,6}]4{3,6}4{6,3}[4(b2+bc+c2){6,3}]2{3,6}b ≡ c mod 3, bc(b − c) > 0
{3,6}[(b2+bc+c2){3,6}]{3,6}{6,3}[(b2+bc+c2){6,3}]{6,3}b ≢ c mod 3
2{3,6}[2(b2+bc+c2){3,6}]2{3,6}2{6,3}[2(b2+bc+c2){6,3}]2{6,3}b ≢ c mod 3, bc(b − c) > 0
{6,3}[2(b2+bc+c2){3,6}][2(b2+bc+c2){6,3}]{3,6}b ≢ c mod 3
2{6,3}[4(b2+bc+c2)2{3,6}][4(b2+bc+c2){6,3}]2{3,6}b ≢ c mod 3, bc(b − c) > 0

A distinction must be made when an integer can be expressed in the forms b2+c2 or b2+bc+c2 in two different ways, e.g. 145 = 122 + 12 = 92 + 82, or 91 = 92 + 9 ⋅ 1 + 12 = 62 + 6 ⋅ 5 + 52. In such cases, Coxeter notates the sum explicitly, e.g. {4,4}[(144+1){4,4}]{4,4} as opposed to {4,4}[(81+64){4,4}]{4,4}. [2]

The following compounds of compact or paracompact hyperbolic tessellations were known to Coxeter in 1964, though a proof of completeness was not then known: [2]

Hyperbolic regular compounds [2]
Self-dual
{4,q}[2{q,q}]{q,4}
{3,8}[6{8,8}]{8,3}
{5,5}[6{10,10}]{5,5}
{4,5}[12{10,10}]{5,4}
{3,7}[9{7,7}]{7,3}
2{3,7}[18{7,7}]2{7,3}
Dual pairs
{3,2q}[3{q,2q}]2{2q,3}2{3,2q}[3{2q,q}]{2q,3}
{4,5}[6{4,10}]2{4,5}2{5,4}[6{10,4}]{5,4}
{3,7}[8{3,14}]2{3,7}2{7,3}[8{14,3}]{7,3}
{3,7}[24{7,14}]2{7,3}2{3,7}[24{14,7}]{7,3}
{3,9}[12{9,18}]2{9,3}2{3,9}[12{18,9}]{9,3}
{2q,q}[2{q,2q}][2{2q,q}]{q,2q}
2{3,7}[9{4,7}][9{7,4}]2{7,3}
{3,9}[4{3,18}][4{18,3}]{9,3}

The Euclidean and hyperbolic compound families {4,q}[2{q,q}]{q,4} appear because h{4,q} = {q,q}, i.e. taking alternate vertices of a {4,q} results in a {q,q}. They are thus the Euclidean and hyperbolic analogues of the spherical stella octangula, which is the q=3 case. [2]

It is also the case that h{2q,q} = {q,2q}, yielding the compound {2q,q}[2{q,2q}] and its dual [2{2q,q}]{q,2q}. Now if we take the dual of the {2q,q}, we obtain a third {q,2q} whose vertices are at the centres of alternate faces of the other two {q,2q}; this gives the compound {3,2q}[3{q,2q}]2{2q,3} and its dual 2{3,2q}[3{2q,q}]{2q,3}. These compounds are hyperbolic if q > 3 and Euclidean if q = 3. These compounds show an analogy to the spherical compounds {4,3,3}[2{3,3,4}], [2{4,3,3}]{3,3,4}, {3,4,3}[3{3,3,4}]2{3,4,3}, and 2{3,4,3}[3{4,3,3}]{3,4,3}. [2]

If one sets q = 8 in {4,q}[2{q,q}]{q,4}, and q = 4 in {3,2q}[3{q,2q}]2{2q,3}, then one obtains the special cases {4,8}[2{8,8}]{8,4} and {3,8}[3{4,8}]2{8,3}. The latter's {4,8}'s can be replaced by pairs of {8,8}'s according to the former, giving the self-dual compound {3,8}[6{8,8}]{8,3}. [2]

A few examples of Euclidean and hyperbolic regular compounds
Self-dualDualsSelf-dual
2 {4,4} 2 {6,3} 2 {3,6} 2 {∞,∞}
Kah 4 4.png Compound 2 hexagonal tilings.png Compound 2 triangular tilings.svg Infinite-order apeirogonal tiling and dual.png
{{4,4}} or a{4,4} or {4,4}[2{4,4}]{4,4}
CDel nodes 10ru.pngCDel split2-44.pngCDel node.png + CDel nodes 01rd.pngCDel split2-44.pngCDel node.png or CDel node h3.pngCDel 4.pngCDel node.pngCDel 4.pngCDel node.png		[2{6,3}]{3,6}a{6,3} or {6,3}[2{3,6}]
CDel branch 10ru.pngCDel split2.pngCDel node.png + CDel branch 01rd.pngCDel split2.pngCDel node.png or CDel node h3.pngCDel 6.pngCDel node.pngCDel 3.pngCDel node.png		{{∞,∞}} or a{∞,∞} or {4,∞}[2{∞,∞}]{∞,4}
CDel labelinfin.pngCDel branch 10ru.pngCDel split2-ii.pngCDel node.png + CDel labelinfin.pngCDel branch 01rd.pngCDel split2-ii.pngCDel node.png or CDel node h3.pngCDel infin.pngCDel node.pngCDel infin.pngCDel node.png
3 {6,3}3 {3,6}3 {∞,∞}
Compound 3 hexagonal tilings.png Compound 3 triangular tilings.svg Iii symmetry 000.png
2{3,6}[3{6,3}]{6,3}{3,6}[3{3,6}]2{6,3}
CDel branch 10ru.pngCDel split2.pngCDel node.png + CDel branch 01rd.pngCDel split2.pngCDel node.png + CDel branch.pngCDel split2.pngCDel node 1.png
CDel labelinfin.pngCDel branch 10ru.pngCDel split2-ii.pngCDel node.png + CDel labelinfin.pngCDel branch 01rd.pngCDel split2-ii.pngCDel node.png + CDel labelinfin.pngCDel branch.pngCDel split2-ii.pngCDel node 1.png

Four dimensional compounds

Orthogonal projections
Regular compound 75 tesseracts.png Regular compound 75 16-cells.png
75 {4,3,3} 75 {3,3,4}

Coxeter lists 32 regular compounds of regular 4-polytopes in his book Regular Polytopes . [3] McMullen adds six in his paper New Regular Compounds of 4-Polytopes, in which he also proves that the list is now complete. [4] In the following tables, the superscript (var) indicates that the labeled compounds are distinct from the other compounds with the same symbols.

Self-dual regular compounds
CompoundConstituentSymmetryVertex arrangementCell arrangement
120 {3,3,3} 5-cell [5,3,3], order 14400 [3] {5,3,3}{3,3,5}
120 {3,3,3} (var) 5-cell order 1200 [4] {5,3,3}{3,3,5}
720 {3,3,3} 5-cell [5,3,3], order 14400 [4] 6{5,3,3}6{3,3,5}
5 {3,4,3} 24-cell [5,3,3], order 14400 [3] {3,3,5}{5,3,3}
Regular compounds as dual pairs
Compound 1Compound 2SymmetryVertex arrangement (1)Cell arrangement (1)Vertex arrangement (2)Cell arrangement (2)
3 {3,3,4} [5] 3 {4,3,3} [3,4,3], order 1152 [3] {3,4,3}2{3,4,3}2{3,4,3}{3,4,3}
15 {3,3,4} 15 {4,3,3} [5,3,3], order 14400 [3] {3,3,5}2{5,3,3}2{3,3,5}{5,3,3}
75 {3,3,4} 75 {4,3,3} [5,3,3], order 14400 [3] 5{3,3,5}10{5,3,3}10{3,3,5}5{5,3,3}
75 {3,3,4} 75 {4,3,3} [5,3,3], order 14400 [3] {5,3,3}2{3,3,5}2{5,3,3}{3,3,5}
75 {3,3,4} 75 {4,3,3} order 600 [4] {5,3,3}2{3,3,5}2{5,3,3}{3,3,5}
300 {3,3,4} 300 {4,3,3} [5,3,3]+, order 7200 [3] 4{5,3,3}8{3,3,5}8{5,3,3}4{3,3,5}
600 {3,3,4} 600 {4,3,3} [5,3,3], order 14400 [3] 8{5,3,3}16{3,3,5}16{5,3,3}8{3,3,5}
25 {3,4,3} 25 {3,4,3} [5,3,3], order 14400 [3] {5,3,3}5{5,3,3}5{3,3,5}{3,3,5}

There are two different compounds of 75 tesseracts: one shares the vertices of a 120-cell, while the other shares the vertices of a 600-cell. It immediately follows therefore that the corresponding dual compounds of 75 16-cells are also different.

Self-dual star compounds
CompoundSymmetryVertex arrangementCell arrangement
5 {5,5/2,5} [5,3,3]+, order 7200 [3] {5,3,3}{3,3,5}
10 {5,5/2,5} [5,3,3], order 14400 [3] 2{5,3,3}2{3,3,5}
5 {5/2,5,5/2} [5,3,3]+, order 7200 [3] {5,3,3}{3,3,5}
10 {5/2,5,5/2} [5,3,3], order 14400 [3] 2{5,3,3}2{3,3,5}
Regular star compounds as dual pairs
Compound 1Compound 2SymmetryVertex arrangement (1)Cell arrangement (1)Vertex arrangement (2)Cell arrangement (2)
5 {3,5,5/2} 5 {5/2,5,3} [5,3,3]+, order 7200 [3] {5,3,3}{3,3,5}{5,3,3}{3,3,5}
10 {3,5,5/2} 10 {5/2,5,3} [5,3,3], order 14400 [3] 2{5,3,3}2{3,3,5}2{5,3,3}2{3,3,5}
5 {5,5/2,3} 5 {3,5/2,5} [5,3,3]+, order 7200 [3] {5,3,3}{3,3,5}{5,3,3}{3,3,5}
10 {5,5/2,3} 10 {3,5/2,5} [5,3,3], order 14400 [3] 2{5,3,3}2{3,3,5}2{5,3,3}2{3,3,5}
5 {5/2,3,5} 5 {5,3,5/2} [5,3,3]+, order 7200 [3] {5,3,3}{3,3,5}{5,3,3}{3,3,5}
10 {5/2,3,5} 10 {5,3,5/2} [5,3,3], order 14400 [3] 2{5,3,3}2{3,3,5}2{5,3,3}2{3,3,5}

There are also fourteen partially regular compounds, that are either vertex-transitive or cell-transitive but not both. The seven vertex-transitive partially regular compounds are the duals of the seven cell-transitive partially regular compounds.

Partially regular compounds as dual pairs
Compound 1
Vertex-transitive 		Compound 2
Cell-transitive 		Symmetry
2 16-cells [6] 2 tesseracts [4,3,3], order 384 [3]
25 24-cell (var)25 24-cell (var)order 600 [4]
100 24-cell 100 24-cell [5,3,3]+, order 7200 [3]
200 24-cell 200 24-cell [5,3,3], order 14400 [3]
5 600-cell 5 120-cell [5,3,3]+, order 7200 [3]
10 600-cell 10 120-cell [5,3,3], order 14400 [3]
Partially regular star compounds as dual pairs
Compound 1
Vertex-transitive 		Compound 2
Cell-transitive 		Symmetry
5 {3,3,5/2} 5 {5/2,3,3} [5,3,3]+, order 7200 [3]
10 {3,3,5/2} 10 {5/2,3,3} [5,3,3], order 14400 [3]

Although the 5-cell and 24-cell are both self-dual, their dual compounds (the compound of two 5-cells and compound of two 24-cells) are not considered to be regular, unlike the compound of two tetrahedra and the various dual polygon compounds, because they are neither vertex-regular nor cell-regular: they are not facetings or stellations of any regular 4-polytope. However, they are vertex-, edge-, face-, and cell-transitive.

Euclidean 3-space compounds

The only regular Euclidean compound honeycombs are an infinite family of compounds of cubic honeycombs, all sharing vertices and faces with another cubic honeycomb. This compound can have any number of cubic honeycombs. The Coxeter notation is {4,3,4}[d{4,3,4}]{4,3,4}.

Hyperbolic 3-space compounds

C. W. L. Garner described two dual pairs of regular hyperbolic compound honeycombs in 1970: the compact pair 2{5,3,4}[5{4,3,5}] and [5{5,3,4}]2{4,3,5}, and the paracompact pair {6,3,3}[5{6,3,4}] and [5{4,3,6}]{3,3,6}. He did not consider vertex-regular compounds where the vertices are at infinity, or (reciprocally) cell-regular compounds where the cells are centred at infinity. [7] In 2019, Peter McMullen (who focused only on the compact case) pointed out and filled a gap in Garner's proof of completeness, so that it is now proven that 2{5,3,4}[5{4,3,5}] and [5{5,3,4}]2{4,3,5} are the only compact regular hyperbolic honeycomb compounds. [8]

Five dimensions and higher compounds

There are no regular compounds in five or six dimensions. There are three known seven-dimensional compounds (16, 240, or 480 7-simplices), and six known eight-dimensional ones (16, 240, or 480 8-cubes or 8-orthoplexes). There is also one compound of n-simplices in n-dimensional space provided that n is one less than a power of two, and also two compounds (one of n-cubes and a dual one of n-orthoplexes) in n-dimensional space if n is a power of two.

The Coxeter notation for these compounds are (using αn = {3n−1}, βn = {3n−2,4}, γn = {4,3n−2}):

The general cases (where n = 2k and d = 22k − k − 1, k = 2, 3, 4, ...):

Euclidean honeycomb compound

A known family of regular Euclidean compound honeycombs in five or more dimensions is an infinite family of compounds of hypercubic honeycombs, all sharing vertices and faces with another hypercubic honeycomb. This compound can have any number of hypercubic honeycombs. The Coxeter notation is δn[dδn]δn where δn = {∞} when n = 2 and {4,3n−3,4} when n ≥ 3.

Hyperbolic honeycomb compounds

In four dimensions, Garner (1970) asserted the existence of {3,3,3,5}[26{5,3,3,5}]{5,3,3,3}; [7] although neither justification nor construction was given, McMullen (2019) proved that this claim is correct. [8] McMullen showed the existence of the following compact compounds: [8]

McMullen conjectures that this list is complete regarding the compact compounds. If any more compact compounds exist, they must involve {4,3,3,5} or {5,3,3,5} being inscribed in {5,3,3,3} (the only case not yet excluded). [8]

In five dimensions, there is only one regular hyperbolic honeycomb whose vertices are not at infinity: {3,4,3,3,3}. Thus there are no regular compounds conforming to Garner's restriction that the vertices of a vertex-regular compound should not be at infinity. In six dimensions or higher, there are no compact or paracompact regular hyperbolic honeycombs at all, and thus no compact or paracompact compounds exist. [7]

See also

Related Research Articles

<span class="mw-page-title-main">Dual polyhedron</span> Polyhedron associated with another by swapping vertices for faces

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

<span class="mw-page-title-main">4-polytope</span> Four-dimensional geometric object with flat sides

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

<span class="mw-page-title-main">Schläfli symbol</span> Notation that defines regular polytopes and tessellations

In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.

<span class="mw-page-title-main">Regular polytope</span> Polytope with highest degree of symmetry

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.

<span class="mw-page-title-main">Tetrahedral-octahedral honeycomb</span> Quasiregular space-filling tesselation

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

<span class="mw-page-title-main">Order-4 dodecahedral honeycomb</span> Regular tiling of hyperbolic 3-space

In hyperbolic geometry, the order-4 dodecahedral honeycomb is one of four compact regular space-filling tessellations of hyperbolic 3-space. With Schläfli symbol {5,3,4}, it has four dodecahedra around each edge, and 8 dodecahedra around each vertex in an octahedral arrangement. Its vertices are constructed from 3 orthogonal axes. Its dual is the order-5 cubic honeycomb.

<span class="mw-page-title-main">Uniform polytope</span> Isogonal polytope with uniform facets

In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. Here, "vertex-transitive" means that it has symmetries taking every vertex to every other vertex; the same must also be true within each lower-dimensional face of the polytope. In two dimensions a stronger definition is used: only the regular polygons are considered as uniform, disallowing polygons that alternate between two different lengths of edges.

In geometry, a complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one.

In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.

<span class="mw-page-title-main">16-cell honeycomb</span>

In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {3,3,4,3}, and constructed by a 4-dimensional packing of 16-cell facets, three around every face.

<span class="mw-page-title-main">Snub (geometry)</span> Geometric operation applied to a polyhedron

In geometry, a snub is an operation applied to a polyhedron. The term originates from Kepler's names of two Archimedean solids, for the snub cube and snub dodecahedron.

In geometry, a skew apeirohedron is an infinite skew polyhedron consisting of nonplanar faces or nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface.

<span class="mw-page-title-main">Uniform 5-polytope</span> Five-dimensional geometric shape

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.

<span class="mw-page-title-main">Regular 4-polytope</span> Four-dimensional analogues of the regular polyhedra in three dimensions

In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.

In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedra which include the possibility of nonplanar faces or vertex figures. Coxeter looked at skew vertex figures which created new 4-dimensional regular polyhedra, and much later Branko Grünbaum looked at regular skew faces.

In geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space. The symbol 521 is from Coxeter, named for the length of the 3 branches of its Coxeter-Dynkin diagram.

<span class="mw-page-title-main">Order-4 square tiling honeycomb</span>

In the geometry of hyperbolic 3-space, the order-4 square tiling honeycomb is one of 11 paracompact regular honeycombs. It is paracompact because it has infinite cells and vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {4,4,4}, it has four square tilings around each edge, and infinite square tilings around each vertex in a square tiling vertex figure.

<span class="mw-page-title-main">Regular skew apeirohedron</span> Infinite regular skew polyhedron

In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron. They have either skew regular faces or skew regular vertex figures.

References

  1. ↑ Coxeter (1973), p. 48.
  2. 1 2 3 4 5 6 7 8 9 Coxeter, H. S. M. (24 March 1964). "Regular compound tessellations of the hyperbolic plane". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 278 (1373): 147–167. Bibcode:1964RSPSA.278..147C. doi:10.1098/rspa.1964.0052.
  3. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 Coxeter (1973). Table VII, p. 305
  4. 1 2 3 4 5 McMullen (2018).
  5. ↑ Klitzing, Richard. "Uniform compound stellated icositetrachoron".
  6. ↑ Klitzing, Richard. "Uniform compound demidistesseract".
  7. 1 2 3 Garner, C. W. L. (1970). "Compound honeycombs in hyperbolic space". Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences. 316 (152): 441–448. Bibcode:1970RSPSA.316..441G. doi:10.1098/rspa.1970.0089.
  8. 1 2 3 4 McMullen, Peter (2019). "Regular compounds of honeycombs in H3 and H4". Advances in Mathematics. 349: 56–83. doi:10.1016/j.aim.2019.04.006 . Retrieved 12 October 2024.

Bibliography

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.