M-theory is a theory in physics that unifies all consistent versions of superstring theory. Edward Witten first conjectured the existence of such a theory at a string theory conference at the University of Southern California in 1995. Witten's announcement initiated a flurry of research activity known as the second superstring revolution. Prior to Witten's announcement, string theorists had identified five versions of superstring theory. Although these theories initially appeared to be very different, work by many physicists showed that the theories were related in intricate and nontrivial ways. Physicists found that apparently distinct theories could be unified by mathematical transformations called S-duality and T-duality. Witten's conjecture was based in part on the existence of these dualities and in part on the relationship of the string theories to a field theory called eleven-dimensional supergravity.
In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than the string scale, a string looks just like an ordinary particle, with its mass, charge, and other properties determined by the vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the graviton, a quantum mechanical particle that carries the gravitational force. Thus, string theory is a theory of quantum gravity.
String field theory (SFT) is a formalism in string theory in which the dynamics of relativistic strings is reformulated in the language of quantum field theory. This is accomplished at the level of perturbation theory by finding a collection of vertices for joining and splitting strings, as well as string propagators, that give a Feynman diagram-like expansion for string scattering amplitudes. In most string field theories, this expansion is encoded by a classical action found by second-quantizing the free string and adding interaction terms. As is usually the case in second quantization, a classical field configuration of the second-quantized theory is given by a wave function in the original theory. In the case of string field theory, this implies that a classical configuration, usually called the string field, is given by an element of the free string Fock space.
In string theory, D-branes, short for Dirichlet membrane, are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes are typically classified by their spatial dimension, which is indicated by a number written after the D. A D0-brane is a single point, a D1-brane is a line, a D2-brane is a plane, and a D25-brane fills the highest-dimensional space considered in bosonic string theory. There are also instantonic D(–1)-branes, which are localized in both space and time.
Bosonic string theory is the original version of string theory, developed in the late 1960s and named after Satyendra Nath Bose. It is so called because it contains only bosons in the spectrum.
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings theories. Type II string theory accounts for two of the five consistent superstring theories in ten dimensions. Both theories have extended supersymmetry which is maximal amount of supersymmetry — namely 32 supercharges — in ten dimensions. Both theories are based on oriented closed strings. On the worldsheet, they differ only in the choice of GSO projection.
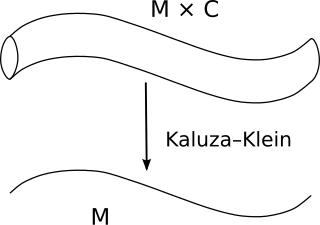
In theoretical physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic.
In theoretical physics and mathematics, a Wess–Zumino–Witten (WZW) model, also called a Wess–Zumino–Novikov–Witten model, is a type of two-dimensional conformal field theory named after Julius Wess, Bruno Zumino, Sergei Novikov and Edward Witten. A WZW model is associated to a Lie group, and its symmetry algebra is the affine Lie algebra built from the corresponding Lie algebra. By extension, the name WZW model is sometimes used for any conformal field theory whose symmetry algebra is an affine Lie algebra.
In theoretical physics, topological string theory is a version of string theory. Topological string theory appeared in papers by theoretical physicists, such as Edward Witten and Cumrun Vafa, by analogy with Witten's earlier idea of topological quantum field theory.
In string theory, K-theory classification refers to a conjectured application of K-theory to superstrings, to classify the allowed Ramond–Ramond field strengths as well as the charges of stable D-branes.
In mathematical physics, a super Virasoro algebra is an extension of the Virasoro algebra to a Lie superalgebra. There are two extensions with particular importance in superstring theory: the Ramond algebra and the Neveu–Schwarz algebra. Both algebras have N = 1 supersymmetry and an even part given by the Virasoro algebra. They describe the symmetries of a superstring in two different sectors, called the Ramond sector and the Neveu–Schwarz sector.
The history of string theory spans several decades of intense research including two superstring revolutions. Through the combined efforts of many researchers, string theory has developed into a broad and varied subject with connections to quantum gravity, particle and condensed matter physics, cosmology, and pure mathematics.
The Type 0 string theory is a less well-known model of string theory. It is a superstring theory in the sense that the worldsheet theory is supersymmetric. However, the spacetime spectrum is not supersymmetric and, in fact, does not contain any fermions at all. In dimensions greater than two, the ground state is a tachyon so the theory is unstable. These properties make it similar to the bosonic string and an unsuitable proposal for describing the world as we observe it, although a GSO projection does get rid of the tachyon and the even G-parity sector of the theory defines a stable string theory. The theory is used sometimes as a toy model for exploring concepts in string theory, notably closed string tachyon condensation. Some other recent interest has involved the two-dimensional Type 0 string which has a non-perturbatively stable matrix model description.
The non-critical string theory describes the relativistic string without enforcing the critical dimension. Although this allows the construction of a string theory in 4 spacetime dimensions, such a theory usually does not describe a Lorentz invariant background. However, there are recent developments which make possible Lorentz invariant quantization of string theory in 4-dimensional Minkowski space-time.
Pierre Ramond is distinguished professor of physics at University of Florida in Gainesville, Florida. He initiated the development of superstring theory.
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modeling them as vibrations of tiny supersymmetric strings.

David Ian Olive ; 16 April 1937 – 7 November 2012) was a British theoretical physicist. Olive made fundamental contributions to string theory and duality theory, he is particularly known for his work on the GSO projection and Montonen–Olive duality.
Higher-dimensional supergravity is the supersymmetric generalization of general relativity in higher dimensions. Supergravity can be formulated in any number of dimensions up to eleven. This article focuses upon supergravity (SUGRA) in greater than four dimensions.
This page is a glossary of terms in string theory, including related areas such as supergravity, supersymmetry, and high energy physics.
In string theory, the Ramond–Neveu–Schwarz (RNS) formalism is an approach to formulating superstrings in which the worldsheet has explicit superconformal invariance but spacetime supersymmetry is hidden, in contrast to the Green–Schwarz formalism where the latter is explicit. It was originally developed by Pierre Ramond, André Neveu and John Schwarz in the RNS model in 1971, which gives rise to type II string theories and can also give type I string theory. Heterotic string theories can also be acquired through this formalism by using a different worldsheet action. There are various ways to quantize the string within this framework including light-cone quantization, old canonical quantization, and BRST quantization. A consistent string theory is only acquired if the spectrum of states is restricted through a procedure known as a GSO projection, with this projection being automatically incorporated in the Green–Schwarz formalism.