History
| | This section is empty. You can help by adding to it. (July 2010) |
The MIT General Circulation Model (MITgcm) is a numerical computer code that solves the equations of motion governing the ocean or Earth's atmosphere using the finite volume method. It was developed at the Massachusetts Institute of Technology and was one of the first non-hydrostatic models of the ocean. It has an automatically generated adjoint that allows the model to be used for data assimilation. The MITgcm is written in the programming language Fortran.
| | This section is empty. You can help by adding to it. (July 2010) |

A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algorithm.
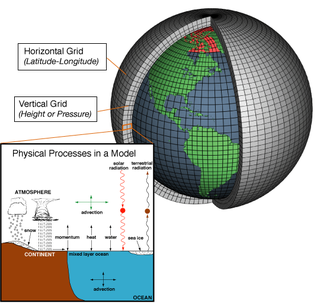
A general circulation model (GCM) is a type of climate model. It employs a mathematical model of the general circulation of a planetary atmosphere or ocean. It uses the Navier–Stokes equations on a rotating sphere with thermodynamic terms for various energy sources. These equations are the basis for computer programs used to simulate the Earth's atmosphere or oceans. Atmospheric and oceanic GCMs are key components along with sea ice and land-surface components.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations. In the finite volume method, volume integrals in a partial differential equation that contain a divergence term are converted to surface integrals, using the divergence theorem. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics packages. "Finite volume" refers to the small volume surrounding each node point on a mesh.
In mathematical logic and theoretical computer science, a register machine is a generic class of abstract machines used in a manner similar to a Turing machine. All models of register machine are Turing equivalent.

Level-set methods (LSM) are a conceptual framework for using level sets as a tool for numerical analysis of surfaces and shapes. The advantage of the level-set model is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects. Also, the level-set method makes it easier to follow shapes that change topology, for example, when a shape splits in two, develops holes, or the reverse of these operations. These characteristics make the level-set method an effective method for modeling time-varying objects, like inflation of an airbag, or a drop of oil floating in water.

Numerical weather prediction (NWP) uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic results. A number of global and regional forecast models are run in different countries worldwide, using current weather observations relayed from radiosondes, weather satellites and other observing systems as inputs.
In hydrology, an oceanic basin (or ocean basin) is anywhere on Earth that is covered by seawater. Geologically, most of the ocean basins are large geologic basins that are below sea level.

Finite-difference time-domain (FDTD) or Yee's method is a numerical analysis technique used for modeling computational electrodynamics. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.

Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.

A geodesic grid is a spatial grid based on a geodesic polyhedron or Goldberg polyhedron.
The Princeton Ocean Model (POM) is a community general numerical model for ocean circulation that can be used to simulate and predict oceanic currents, temperatures, salinities and other water properties. POM-WEB and POMusers.org

The history of numerical weather prediction considers how current weather conditions as input into mathematical models of the atmosphere and oceans to predict the weather and future sea state has changed over the years. Though first attempted manually in the 1920s, it was not until the advent of the computer and computer simulation that computation time was reduced to less than the forecast period itself. ENIAC was used to create the first forecasts via computer in 1950, and over the years more powerful computers have been used to increase the size of initial datasets and use more complicated versions of the equations of motion. The development of global forecasting models led to the first climate models. The development of limited area (regional) models facilitated advances in forecasting the tracks of tropical cyclone as well as air quality in the 1970s and 1980s.

Gerris is computer software in the field of computational fluid dynamics (CFD). Gerris was released as free and open-source software, subject to the requirements of the GNU General Public License (GPL), version 2 or any later.
The Flow-following, finite-volume Icosahedral Model (FIM) is an experimental numerical weather prediction model that was developed at the Earth System Research Laboratory in the United States from 2008 to 2016.
Ocean general circulation models (OGCMs) are a particular kind of general circulation model to describe physical and thermodynamical processes in oceans. The oceanic general circulation is defined as the horizontal space scale and time scale larger than mesoscale. They depict oceans using a three-dimensional grid that include active thermodynamics and hence are most directly applicable to climate studies. They are the most advanced tools currently available for simulating the response of the global ocean system to increasing greenhouse gas concentrations. A hierarchy of OGCMs have been developed that include varying degrees of spatial coverage, resolution, geographical realism, process detail, etc.

The Finite Volume Community Ocean Model is a prognostic, unstructured-grid, free-surface, 3-D primitive equation coastal ocean circulation model. The model is developed primarily by researchers at the University of Massachusetts Dartmouth and Woods Hole Oceanographic Institution, and used by researchers worldwide. Originally developed for the estuarine flooding/drying process, FVCOM has been upgraded to the spherical coordinate system for basin and global applications.
John Charles Marshall, FRS is a British oceanographer and academic. He is the Cecil and Ida Green Professor of Oceanography in the Department of Earth, Atmospheric and Planetary Sciences at the Massachusetts Institute of Technology (MIT). He is also an adjunct senior research scientist in the Department of Applied Physics and Applied Mathematics at Columbia University.
FESOM is a multi-resolution ocean general circulation model that solves the equations of motion describing the ocean and sea ice using finite-element and finite-volume methods on unstructured computational grids. The model is developed and supported by researchers at the Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research (AWI), in Bremerhaven, Germany.

In geology, numerical modeling is a widely applied technique to tackle complex geological problems by computational simulation of geological scenarios.