Magnetic space group

In solid state physics, the magnetic space groups, or Shubnikov groups, are the symmetry groups which classify the symmetries of a crystal both in space, and in a two-valued property such as electron spin. To represent such a property, each lattice point is colored black or white, ^[1] and in addition to the usual three-dimensional symmetry operations, there is a so-called "antisymmetry" operation which turns all black lattice points white and all white lattice points black. Thus, the magnetic space groups serve as an extension to the crystallographic space groups which describe spatial symmetry alone.

The application of magnetic space groups to crystal structures is motivated by Curie's Principle. Compatibility with a material's symmetries, as described by the magnetic space group, is a necessary condition for a variety of material properties, including ferromagnetism, ferroelectricity, topological insulation.

History

A major step was the work of Heinrich Heesch, who first rigorously established the concept of antisymmetry as part of a series of papers in 1929 and 1930. ^{[2] [3] [4] [5]} Applying this antisymmetry operation to the 32 crystallographic point groups gives a total of 122 magnetic point groups. ^{[6] [7]} However, although Heesch correctly laid out each of the magnetic point groups, his work remained obscure, and the point groups were later re-derived by Tavger and Zaitsev. ^[8] The concept was more fully explored by Shubnikov in terms of color symmetry. ^[9] When applied to space groups, the number increases from the usual 230 three dimensional space groups to 1651 magnetic space groups, ^[10] as found in the 1953 thesis of Alexandr Zamorzaev. ^{[11] [12] [13]} While the magnetic space groups were originally found using geometry, it was later shown the same magnetic space groups can be found using generating sets. ^[14]

Description

Magnetic space groups

The magnetic space groups can be placed into three categories. First, the 230 colorless groups contain only spatial symmetry, and correspond to the crystallographic space groups. Then there are 230 grey groups, which are invariant under antisymmetry. Finally are the 1191 black-white groups, which contain the more complex symmetries. There are two common conventions for giving names to the magnetic space groups. They are Opechowski-Guiccione (named after Wladyslaw Opechowski and Rosalia Guiccione) ^[15] and Belov-Neronova-Smirnova. ^[10] For colorless and grey groups, the conventions use the same names, but they treat the black-white groups differently. A full list of the magnetic space groups (in both conventions) can be found both in the original papers, and in several places online. ^{[16] [17] [18]}

Types of magnetic space groups ^[19]

Type	Name	Number of groups	Description
Type I	Colorless groups	230	Ordinary crystallographic space groups, without any additional symmetry.
Type II	Grey groups	230	Space groups, with an additional anti-symmetry version of every symmetry operation.
Type III	Black-White groups (ordinary Bravais lattices)	674	Space groups, with additional anti-symmetry versions of half of the symmetry operations.
Type IV	Black-White groups (black-white Bravais Lattices)	517	Space groups, with additional combined spatial translation-time reversal symmetry.

The types can be distinguished by their different construction. ^[19] Type I magnetic space groups, ${\displaystyle {\mathcal {M}}_{I}}$ are identical to the ordinary space groups,${\displaystyle G}$.

${\displaystyle {\mathcal {M}}_{I}=G}$

Type II magnetic space groups, ${\displaystyle {\mathcal {M}}_{II}}$, are made up of all the symmetry operations of the crystallographic space group, ${\displaystyle G}$, plus the product of those operations with time reversal operation, ${\displaystyle {\mathcal {T}}}$. Equivalently, this can be seen as the direct product of an ordinary space group with the point group ${\displaystyle 1'}$.

${\displaystyle {\mathcal {M}}_{II}=G+{\mathcal {T}}G}$

${\displaystyle {\mathcal {M}}_{II}=G\times 1'}$

Type III magnetic space groups, ${\displaystyle {\mathcal {M}}_{III}}$, are constructed using a group ${\displaystyle H}$, which is a subgroup of ${\displaystyle G}$ with index 2.

${\displaystyle {\mathcal {M}}_{III}=H+{\mathcal {T}}(G-H)}$

Type IV magnetic space groups, ${\displaystyle {\mathcal {M}}_{IV}}$, are constructed with the use of a pure translation, ${\displaystyle \{E|t_{0}\}}$, which is Seitz notation ^[20] for null rotation and a translation, ${\displaystyle t_{0}}$. Here the ${\displaystyle t_{0}}$ is a vector (usually given in fractional coordinates) pointing from a black colored point to a white colored point, or vice versa.

${\displaystyle {\mathcal {M}}_{IV}=G+{\mathcal {T}}\{E|t_{0}\}G}$

Magnetic point groups

The following table lists all of the 122 possible three-dimensional magnetic point groups. This is given in the short version of Hermann–Mauguin notation in the following table. Here, the addition of an apostrophe to a symmetry operation indicates that the combination of the symmetry element and the antisymmetry operation is a symmetry of the structure. There are 32 Crystallographic point groups, 32 grey groups, and 58 magnetic point groups. ^[21]

Crystallographic point groups	Grey point groups	Magnetic point groups
1	1'
1	11'	1'
2	21'	2'
m	m1'	m'
2/m	2/m1'	2'/m'	2/m'	2'/m
222	2221'	2'2'2
mm2	mm21'	m'm'2	2'm'm
mmm	mmm1'	mm'm'	m'm'm'	mmm'
4	41'	4'
4	41'	4'
4/m	4/m1'	4'/m	4/m'	4'/m'
422	4221'	4'22'	42'2'
4mm	4mm1'	4'mm'	4m'm'
42m	42m1'	4'2m'	4'm2'	42'm'
4/mmm	4/mmm1'	4'/mmm'	4/mm'm'	4/m'm'm'	4/m'mm	4'/m'm'm
3	31'
3	31'	3'
32	321'	32'
3m	3m1'	3m'
3m	3m1'	3m'	3'm'	3'm
6	61'	6'
6	61'	6'
6/m	6/m1'	6'/m'	6/m'	6'/m
622	6221'	6'22'	62'2'
6mm	6mm1'	6'mm'	6m'm'
6m2	6m21'	6'2m'	6'm2'	6m'2'
6/mmm	6/mmm1'	6'/m'mm'	6/mm'm'	6/m'm'm'	6/m'mm	6'/mmm'
23	231'
m3	m31'	m'3'
432	4321'	4'32'
43m	43m1'	4'3m'
m3m	m3m1'	m3m'	m'3'm'	m'3'm

The magnetic point groups which are compatible with ferromagnetism are colored cyan, the magnetic point groups which are compatible with ferroelectricity are colored red, and the magnetic point groups which are compatible with both ferromagnetism and ferroelectricity are purple. ^[22] There are 31 magnetic point groups which are compatible with ferromagnetism. These groups, sometimes called admissible, leave at least one component of the spin invariant under operations of the point group. There are 31 point groups compatible with ferroelectricity; these are generalizations of the crystallographic polar point groups. There are also 31 point groups compatible with the theoretically proposed ferrotorodicity. Similar symmetry arguments have been extended to other electromagnetic material properties such as magnetoelectricity or piezoelectricity. ^[23]

The following diagrams show the stereographic projection of most of the magnetic point groups onto a flat surface. Not shown are the grey point groups, which look identical to the ordinary crystallographic point groups, except they are also invariant under the antisymmetry operation.

1				1	1'
2	2'			m	m'
2/m	2/m'	2'/m	2'/m'
222	2'2'2		mm2	m'm'2	mm'2'
mmm	m'm'm'	mmm'	m'm'm
4	4'			4	4'
4/m	4/m'	4'/m'	4/m'
422	4'22'	42'2'
4mm	4m'm'	4'mm'
42m	42'm'	4'2m'	4'2'm
4/mmm	4/m'm'm'	4/m'mm	4'/mmm'	4'/m'm'm	4/mm'm'
3				3	3'
32	32'			3m	3m'
3m	3m'	3'm'	3'm
6	6'			6	6'
6/m	6/m'	6'/m'	6/m'
622	62'2'	6'2'2
6mm	6m'm'	6'mm'
6m2	6m'2'	6'm2'	6'm'2
6/mmm	6'/mmm'	6'/m'mm'	6/m'm'm'	6/m'mm	6/mm'm'
23				m3	m'3'
432	4'32'			43m	4'3m'
m3m	m'3'm'	m'3'm	m3m'

Black-white Bravais lattices

The black-white Bravais lattices characterize the translational symmetry of the structure like the typical Bravais lattices, but also contain additional symmetry elements. For black-white Bravais lattices, the number of black and white sites is always equal. ^[24] There are 14 traditional Bravais lattices, 14 grey lattices, and 22 black-white Bravais lattices, for a total of 50 two-color lattices in three dimensions. ^[25]

Magnetic (black-white) Bravais lattices ^{[26] [27] [28]}

Triclinic lattice system
Monoclinic lattice system
Orthorhombic lattice system
Tetragonal lattice system
Hexagonal crystal family
Hexagonal lattice system		Rhombohedral lattice system
Cubic lattice system

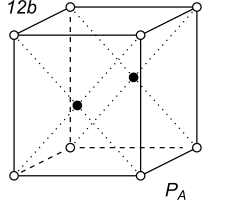
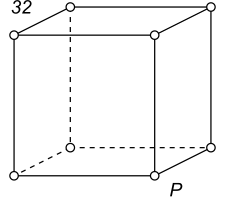
The table shows the 36 black-white Bravais lattices, including the 14 traditional Bravais lattices, but excluding the 14 gray lattices which look identical to the traditional lattices. The lattice symbols are those used for the traditional Bravais lattices. The suffix in the symbol indicates the mode of centering by the black (antisymmetry) points in the lattice, where s denotes edge centering.

Magnetic superspace groups

See also: Superstructure (condensed matter)

When the periodicity of the magnetic order coincides with the periodicity of crystallographic order, the magnetic phase is said to be commensurate, and can be well-described by a magnetic space group. However, when this is not the case, the order does not correspond to any magnetic space group. These phases can instead be described by magnetic superspace groups, which describe incommensurate order. ^[29] This is the same formalism often used to describe the ordering of some quasicrystals.

Phase transitions

The Landau theory of second-order phase transitions has been applied to magnetic phase transitions. The magnetic space group of disordered structure, ${\displaystyle G_{0}}$, transitions to the magnetic space group of the ordered phase, ${\displaystyle G_{1}}$. ${\displaystyle G_{1}}$ is a subgroup of ${\displaystyle G_{0}}$, and keeps only the symmetries which have not been broken during the phase transition. This can be tracked numerically by evolution of the order parameter, which belongs to a single irreducible representation of ${\displaystyle G_{0}}$. ^[30]

Important magnetic phase transitions include the paramagnetic to ferromagnetic transition at the Curie temperature and the paramagnetic to antiferromagnetic transition at the Néel temperature. Differences in the magnetic phase transitions explain why Fe₂O₃, MnCO₃, and CoCO₃ are weakly ferromagnetic, whereas the structurally similar Cr₂O₃ and FeCO₃ are purely antiferromagnetic. ^[31] This theory developed into what is now known as antisymmetric exchange.

A related scheme is the classification of Aizu species which consist of a prototypical non-ferroic magnetic point group, the letter "F" for ferroic, and a ferromagnetic or ferroelectric point group which is a subgroup of the prototypical group which can be reached by continuous motion of the atoms in the crystal structure. ^{[32] [33]}

Applications and extensions

The main application of these space groups is to magnetic structure, where the black/white lattice points correspond to spin up/spin down configuration of electron spin. More abstractly, the magnetic space groups are often thought of as representing time reversal symmetry. ^[34] This is in contrast to time crystals, which instead have time translation symmetry. In the most general form, magnetic space groups can represent symmetries of any two valued lattice point property, such as positive/negative electrical charge or the alignment of electric dipole moments. The magnetic space groups place restrictions on the electronic band structure of materials. Specifically, they place restrictions on the connectivity of the different electron bands, which in turn defines whether material has symmetry-protected topological order. Thus, the magnetic space groups can be used to identify topological materials, such as topological insulators. ^{[35] [36] [37]}

Experimentally, the main source of information about magnetic space groups is neutron diffraction experiments. The resulting experimental profile can be matched to theoretical structures by Rietveld refinement ^[38] or simulated annealing. ^[39]

Adding the two-valued symmetry is also a useful concept for frieze groups which are often used to classify artistic patterns. In that case, the 7 frieze groups with the addition of color reversal become 24 color-reversing frieze groups. ^[40] Beyond the simple two-valued property, the idea has been extended further to three colors in three dimensions, ^[41] and to even higher dimensions and more colors. ^[42]

See also

• Space group
• Magnetic structure
• Group theory

References

1. Gábor Gévay (2000). "Black-and-White Symmetry, Magnetic Symmetry, Self-Duality and Antiprismatic Symmetry: The Common Mathematical Background" (PDF). Forma. 15: 57–60.
2. Heesch, H. (1929-01-01). "Zur Strukturtheorie der ebenen Symmetriegruppen" [Structure theory of plane symmetry groups]. Zeitschrift für Kristallographie - Crystalline Materials (in German). 71 (1–6): 95–102. doi:10.1524/zkri.1929.71.1.95. ISSN   2196-7105. S2CID   102004261.
3. Heesch, H. (1930-01-01). "Zur systematischen Strukturtheorie. II" [Systematic structure theory II]. Zeitschrift für Kristallographie - Crystalline Materials (in German). 72 (1–6): 177–201. doi:10.1524/zkri.1930.72.1.177. ISSN   2196-7105. S2CID   101972126.
4. Heesch, H. (1930). "Zur systematischen Strukturtheorie. III - Über die vierdimensionalen Gruppen des dreidimensionalen Raumes" [Systematic Structure theory III - On the four-dimensional groups of three-dimensional space]. Zeitschrift für Kristallographie - Crystalline Materials (in German). 73 (1–6): 325–345. doi:10.1524/zkri.1930.73.1.325. ISSN   2196-7105. S2CID   102161514.
5. Heesch, H. (1930-01-01). "Zur systematischen Strukturtheorie. IV - Über die Symmetrien zweiter Art in Kontinuen und Remidiskontinuen" [Systematic structure theory IV - On the symmetry of the second kind in continua and semicontinua]. Zeitschrift für Kristallographie - Crystalline Materials (in German). 73 (1–6): 346–356. doi:10.1524/zkri.1930.73.1.346. ISSN   2196-7105. S2CID   102161512.
6. Wills, Andrew S. (2017). "A historical introduction to the symmetries of magnetic structures. Part 1. Early quantum theory, neutron powder diffraction and the coloured space groups". Powder Diffraction. 32 (2): 148–155. arXiv: 1609.09666 . Bibcode:2017PDiff..32..148W. doi:10.1017/S0885715617000124. ISSN   0885-7156. S2CID   118533941.
7. Pantulu, P. V.; Radhakrishna, S. (1967). "A method of deriving shubnikov groups". Proceedings of the Indian Academy of Sciences A. 66 (2): 107–111. doi:10.1007/BF03049452. ISSN   0370-0089. S2CID   118874086.
8. Tavger, B.A.; Zaitsev, V.M. (1956). "Magnetic Symmetry of Crystals" (PDF). Journal of Experimental and Theoretical Physics. 3 (3): 430.
9. A. V. Shubnikov; N. V. Belov (1964). Colored Symmetry . New York, Macmillan.
10. Grimmer, Hans (2009). "Comments on tables of magnetic space groups". Acta Crystallographica Section A. 65 (2): 145–155. Bibcode:2009AcCrA..65..145G. doi:10.1107/S0108767308039007. ISSN   0108-7673. PMID   19225196.
11. Zamorzaev, A. M. (1953). Generalization of the Fedorov groups (PhD) (in Russian). Leningrad State University.
12. "Generalization of the Fedorov groups". Kristallografiya. 2: 15–20. 1957.
13. "Generalization of the Fedorov groups". Soviet Physics Crystallography. 2: 10–15.
14. Kim, Shoon K. (1986). "The 38 assemblies of the general generator sets for 1421 magnetic double space groups". Journal of Mathematical Physics. 27 (5). AIP Publishing: 1484–1489. Bibcode:1986JMP....27.1484K. doi:10.1063/1.527397. ISSN   0022-2488.
15. Opechowski, W.; Guccione, R. (1965). "Magnetic Symmetry". In Rado, George T.; Suhl, Harry (eds.). Magnetism. Vol. 2A. New York: Academic Press. OCLC   31184704.
16. Harold T. Stokes; Branton J. Campbell. "ISO-MAG Table of Magnetic Space Groups" . Retrieved 14 Apr 2019.
17. "Magnetic Space Groups List". University of the Basque Country - Bilbao Crystallographic Server. Retrieved 14 Apr 2019.
18. Litvin, D. B. (2013). Litvin, D. B (ed.). Magnetic Group Tables: 1-, 2-, and 3-Dimensional Magnetic Subperiodic Groups and Magnetic Space Groups. International Union of Crystallography. doi:10.1107/9780955360220001. ISBN   978-0-9553602-2-0.
19. Bradley, C. J.; Cracknell, A. P. (2010). "The Magnetic Groups and their corepresentations". The mathematical theory of symmetry in solids : representation theory for point groups and space groups. Oxford New York: Clarendon Press. pp. 569–681. ISBN   978-0-19-958258-7. OCLC   859155300.
20. Litvin, Daniel B.; Kopský, Vojtěch (2011-05-26). "Seitz notation for symmetry operations of space groups". Acta Crystallographica Section A. 67 (4). International Union of Crystallography (IUCr): 415–418. Bibcode:2011AcCrA..67..415L. doi:10.1107/s010876731101378x. ISSN   0108-7673. PMID   21694481.
21. DeGraef, Marc. Teaching crystallographic andmagnetic point group symmetry using three-dimensional rendered visualizations (PDF). Retrieved 2020-01-17.
22. Schmid, Hans (1973). "On a magnetoelectric classification of materials". International Journal of Magnetism. 4 (4): 337–361.
23. Schmid, Hans (2008-10-09). "Some symmetry aspects of ferroics and single phase multiferroics". Journal of Physics: Condensed Matter. 20 (43). IOP Publishing: 434201. Bibcode:2008JPCM...20Q4201S. doi:10.1088/0953-8984/20/43/434201. ISSN   0953-8984. S2CID   120569385.
24. Laughlin, D. E.; Willard, M. A.; McHenry, M. E. (2000). "Magnetic Ordering: Some Structural Aspects". In Gonis, Antonios; Turchi, Patrice E. A. (eds.). Phase transformations and evolution in materials : proceedings of a symposium sponsored by the Alloy Phase Committee of the joint IMPMD/SMD of the Minerals, Metals, and Materials Society (TMS), held at the 2000 TMS Annual Meeting in Nashville, Tennessee, USA, March 12-16, 2000 (PDF). Warrendale, Pa: TMS. pp. 121–137. ISBN   978-0-87339-468-0. OCLC   44883836.
25. Atoji, Masao (1965). "Graphical Representations of Magnetic Space Groups". American Journal of Physics. 33 (3). American Association of Physics Teachers (AAPT): 212–219. Bibcode:1965AmJPh..33..212A. doi:10.1119/1.1971375. ISSN   0002-9505.
26. Belov, N.V.; Neronova, N. N.; Smirnova, T. S. (1957). "Shubnikov groups". Soviet Physics Crystallography. 2 (3). American Institute of Physics: 311–322. ISSN   0038-5638.
27. Bradley, C. J.; Cracknell, A.P. (1972). "The magnetic groups and their corepresentations". The mathematical theory of symmetry in solids: representation theory for point groups and space groups. Oxford: Oxford University Press. pp. 586–587.
28. Mackay, A.L. (1957). "Extensions of space-group theory". Acta Crystallographica. 10 (9). International Union of Crystallography: 543–548. Bibcode:1957AcCry..10..543M. doi:10.1107/S0365110X57001966.
29. Perez-Mato, J M; Ribeiro, J L; Petricek, V; Aroyo, M I (2012-03-26). "Magnetic superspace groups and symmetry constraints in incommensurate magnetic phases". Journal of Physics: Condensed Matter. 24 (16). IOP Publishing: 163201. arXiv: 1107.2358 . Bibcode:2012JPCM...24p3201P. doi:10.1088/0953-8984/24/16/163201. ISSN   0953-8984. PMID   22447842. S2CID   11738423.
30. Dimmock, John O. (1963-05-15). "Use of Symmetry in the Determination of Magnetic Structures". Physical Review. 130 (4). American Physical Society (APS): 1337–1344. Bibcode:1963PhRv..130.1337D. doi:10.1103/physrev.130.1337. ISSN   0031-899X.
31. Dzyaloshinsky, I. (1958). "A thermodynamic theory of "weak" ferromagnetism of antiferromagnetics". Journal of Physics and Chemistry of Solids. 4 (4). Elsevier BV: 241–255. Bibcode:1958JPCS....4..241D. doi:10.1016/0022-3697(58)90076-3. ISSN   0022-3697.
32. Aizu, Kêitsiro (1970-08-01). "Possible Species of Ferromagnetic, Ferroelectric, and Ferroelastic Crystals". Physical Review B. 2 (3). American Physical Society (APS): 754–772. Bibcode:1970PhRvB...2..754A. doi:10.1103/physrevb.2.754. ISSN   0556-2805.
33. Litvin, D. B. (2008-02-19). "Ferroic classifications extended to ferrotoroidic crystals". Acta Crystallographica Section A. 64 (2). International Union of Crystallography (IUCr): 316–320. Bibcode:2008AcCrA..64..316L. doi:10.1107/s0108767307068262. ISSN   0108-7673. PMID   18285626.
34. Lev Landau; Evgeny Lifshitz (1960). Electrodynamics of Continuous Media. A Course of Theoretical Physics. Vol. 8. Pergamon Press. pp.  116–119. ISBN   978-0750626347.
35. Elcoro, Luis; Wieder, Benjamin J.; Song, Zhida; Xu, Yuanfeng; Bradlyn, Barry; Bernevig, B. Andrei (2021). "Magnetic Topological Quantum Chemistry". Nature Communications. 12 (1). Nature Research: 5965. arXiv: 2010.00598 . Bibcode:2021NatCo..12.5965E. doi:10.1038/s41467-021-26241-8. PMC   8514474 . PMID   34645841.
36. Watanabe, Haruki; Po, Hoi Chun; Vishwanath, Ashvin (2018). "Structure and topology of band structures in the 1651 magnetic space groups". Science Advances. 4 (8). American Association for the Advancement of Science (AAAS): eaat8685. arXiv: 1707.01903 . Bibcode:2018SciA....4.8685W. doi:10.1126/sciadv.aat8685. ISSN   2375-2548. PMC   6070365 . PMID   30083612. S2CID   51910083.
37. Xu, Yuanfeng; Elcoro, Luis; Song, Zhida; Wieder, Benjamin. J.; Vergniory, M. G.; Regnault, Nicolas; Chen, Yulin; Felser, Claudia; Bernevig, B. Andrei (2020). "High-throughput calculations of magnetic topological materials". Nature. 586 (7831): 702–707. arXiv: 2003.00012 . doi:10.1038/s41586-020-2837-0. PMID   33116291. S2CID   226036258.
38. Rietveld, H. M. (1969-06-02). "A profile refinement method for nuclear and magnetic structures". Journal of Applied Crystallography. 2 (2). International Union of Crystallography (IUCr): 65–71. Bibcode:1969JApCr...2...65R. doi:10.1107/s0021889869006558. ISSN   0021-8898.
39. Rodríguez-Carvajal, Juan (1993). "Recent advances in magnetic structure determination by neutron powder diffraction". Physica B: Condensed Matter. 192 (1–2). Elsevier BV: 55–69. Bibcode:1993PhyB..192...55R. doi:10.1016/0921-4526(93)90108-i. ISSN   0921-4526.
40. David A. James; Loukas N. Kalisperis; Alice V. James (2003). The Mathematics of Color-Reversing Decorative Friezes: Faaçdes of Pirgí, Greece (PDF). Bridges: Mathematical Connections in Art, Music, and Science. The International Society of the Arts, Mathematics, and Architecture. p. 135.
41. Harker, D. (1981). "The three-colored three-dimensional space groups". Acta Crystallographica Section A. 37 (3): 286–292. Bibcode:1981AcCrA..37..286H. doi:10.1107/S0567739481000697. ISSN   0567-7394.
42. Koptsik, V. A. (1994). A. S. Marfunin (ed.). General Results of Crystal Structure Analysis of Minerals. Springer Verlag Berlin Heidelberg. pp. 50–55. ISBN   978-3-642-78525-2.

External links

• "MAGNDATA: A collection of magnetic structures with portable cif-type files". University of the Basque Country . Retrieved 2020-01-22.
• "Database of Magnetic Structures Determined by Neutron Diffraction". AGH University of Science and Technology . Retrieved 2020-01-22.