The Okumura model is a radio propagation model that was built using data collected in the city of Tokyo, Japan. The model is ideal for using in cities with many urban structures but not many tall blocking structures. The model served as a base for the Hata model.
The Okumura model was built into three modes: for urban, suburban and open areas. The model for urban areas was built first, and used as the base for the others.
The Okumura model is formally expressed as:
where,
L = The median path loss. Unit: decibel (dB)
LFSL = The free space loss. Unit: decibel (dB).
AMU = Median attenuation. Unit: decibel (dB).
HMG = Mobile station antenna height gain factor
HBG = Base station antenna height gain factor
Kcorrection = Correction factor gain (such as type of environment, water surfaces, isolated obstacle etc.)
Okumura's model is one of the most widely used models for signal prediction in urban areas. This model is applicable for frequencies in the range 150–1920 MHz (although it is typically extrapolated up to 3000 MHz) and distances of 1–100 km. It can be used for base-station antenna heights ranging from 30–1000 m.
Okumura developed a set of curves giving the median attenuation relative to free space (Amu), in an urban area over a quasi-smooth terrain with a base station effective antenna height (hte) of 200 m and a mobile antenna height (hre) of 3 m. These curves were developed from extensive measurements using vertical omni-directional antennas at both the base and mobile, and are plotted as a function of frequency in the range 100–1920 MHz and as a function of distance from the base station in the range 1–100 km. To determine path loss using Okumura's model, the free space path loss between the points of interest is first determined, and then the value of Amu(f, d) (as read from the curves) is added to it along with correction factors to account for the type of terrain. The model can be expressed as:
where L50 is the 50th percentile (i.e., median) value of propagation path loss, LF is the free space propagation loss, Amu is the median attenuation relative to free space, G(hte) is the base station antenna height gain factor, G(hre) is the mobile antenna height gain factor, and GAREA is the gain due to the type of environment. Note that the antenna height gains are strictly a function of height and have nothing to do with antenna patterns.
Plots of Amu(f, d) and GAREA for a wide range of frequencies are shown in Figure 3,23 and Figure 3.24. Furthermore, Okumura found that G(hte) varies at a rate of 20 dB/decade and G(hre) varies at a rate of 10 dB/decade for heights less than 3 m.
Other corrections may also be applied to Okumura's model. Some of the important terrain related parameters are the terrain undulation height (A/i), isolated ridge height, average slope of the terrain and the mixed land-sea parameter. Once the terrain related parameters are calculated, the necessary correction factors can be added or subtracted as required. All these correction factors are also available as Okumura curves [0ku68].
In irregular terrain, one frequently encounters non-line-of-sight paths caused by terrain obstacles. Okumura's model includes a correction factor called the "Isolated Ridge" factor to account for obstacles. However, the applicability of this correction is only to obstacles conforming to that description; i.e. an isolated ridge. More complex terrain cannot be modeled by the Isolated Ridge correction factor. A number of more general models exist [1] [2] [3] [4] [5] [6] for calculating diffraction loss. However, none of these can be applied directly to Okumura's basic mean attenuation. Proprietary methods of doing so have been developed; however, none are known to be in the public domain.
Okumura's model is wholly based on measured data and does not provide any analytical explanation. For many situations, extrapolations of the derived curves can be made to obtain values outside the measurement range, although the validity of such extrapolations depends on the circumstances and the smoothness of the curve in question.
Okumura's model is considered to be among the simplest and best in terms of accuracy in path loss prediction for mature cellular and land mobile radio systems in cluttered environments. It is very practical and has become a standard for system planning in modern land mobile radio systems in Japan. The major disadvantage with the model is its slow response to rapid changes in terrain, therefore the model is fairly good in urban and suburban areas, but not as good in rural areas. Common standard deviations between predicted and measured path loss values are around 10 dB to 14 dB.
In telecommunication, the free-space path loss (FSPL) is the attenuation of radio energy between the feedpoints of two antennas that results from the combination of the receiving antenna's capture area plus the obstacle-free, line-of-sight (LoS) path through free space. The "Standard Definitions of Terms for Antennas", IEEE Std 145-1993, defines free-space loss as "The loss between two isotropic radiators in free space, expressed as a power ratio." It does not include any power loss in the antennas themselves due to imperfections such as resistance. Free-space loss increases with the square of distance between the antennas because the radio waves spread out by the inverse square law and decreases with the square of the wavelength of the radio waves. The FSPL is rarely used standalone, but rather as a part of the Friis transmission formula, which includes the gain of antennas. It is a factor that must be included in the power link budget of a radio communication system, to ensure that sufficient radio power reaches the receiver such that the transmitted signal is received intelligibly.
Path loss, or path attenuation, is the reduction in power density (attenuation) of an electromagnetic wave as it propagates through space. Path loss is a major component in the analysis and design of the link budget of a telecommunication system.
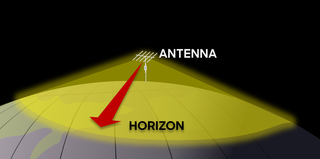
Line-of-sight propagation is a characteristic of electromagnetic radiation or acoustic wave propagation which means waves can only travel in a direct visual path from the source to the receiver without obstacles. Electromagnetic transmission includes light emissions traveling in a straight line. The rays or waves may be diffracted, refracted, reflected, or absorbed by the atmosphere and obstructions with material and generally cannot travel over the horizon or behind obstacles.
Radio propagation is the behavior of radio waves as they travel, or are propagated, from one point to another in vacuum, or into various parts of the atmosphere. As a form of electromagnetic radiation, like light waves, radio waves are affected by the phenomena of reflection, refraction, diffraction, absorption, polarization, and scattering. Understanding the effects of varying conditions on radio propagation has many practical applications, from choosing frequencies for amateur radio communications, international shortwave broadcasters, to designing reliable mobile telephone systems, to radio navigation, to operation of radar systems.
Effective radiated power (ERP), synonymous with equivalent radiated power, is an IEEE standardized definition of directional radio frequency (RF) power, such as that emitted by a radio transmitter. It is the total power in watts that would have to be radiated by a half-wave dipole antenna to give the same radiation intensity as the actual source antenna at a distant receiver located in the direction of the antenna's strongest beam. ERP measures the combination of the power emitted by the transmitter and the ability of the antenna to direct that power in a given direction. It is equal to the input power to the antenna multiplied by the gain of the antenna. It is used in electronics and telecommunications, particularly in broadcasting to quantify the apparent power of a broadcasting station experienced by listeners in its reception area.
In telecommunications, particularly in radio frequency engineering, signal strength refers to the transmitter power output as received by a reference antenna at a distance from the transmitting antenna. High-powered transmissions, such as those used in broadcasting, are expressed in dB-millivolts per metre (dBmV/m). For very low-power systems, such as mobile phones, signal strength is usually expressed in dB-microvolts per metre (dBμV/m) or in decibels above a reference level of one milliwatt (dBm). In broadcasting terminology, 1 mV/m is 1000 μV/m or 60 dBμ.
A link budget is an accounting of all of the power gains and losses that a communication signal experiences in a telecommunication system; from a transmitter, through a communication medium such as radio waves, cable, waveguide, or optical fiber, to the receiver. It is an equation giving the received power from the transmitter power, after the attenuation of the transmitted signal due to propagation, as well as the antenna gains and feedline and other losses, and amplification of the signal in the receiver or any repeaters it passes through. A link budget is a design aid, calculated during the design of a communication system to determine the received power, to ensure that the information is received intelligibly with an adequate signal-to-noise ratio. Randomly varying channel gains such as fading are taken into account by adding some margin depending on the anticipated severity of its effects. The amount of margin required can be reduced by the use of mitigating techniques such as antenna diversity or multiple-input and multiple-output (MIMO).
Non-line-of-sight (NLOS) radio propagation occurs outside of the typical line-of-sight (LOS) between the transmitter and receiver, such as in ground reflections. Near-line-of-sight conditions refer to partial obstruction by a physical object present in the innermost Fresnel zone.
The Egli model is a terrain model for radio frequency propagation. This model, which was first introduced by John Egli in his 1957 paper, was derived from real-world data on UHF and VHF television transmissions in several large cities. It predicts the total path loss for a point-to-point link. Typically used for outdoor line-of-sight transmission, this model provides the path loss as a single quantity.
The ITU terrain loss model is a radio propagation model that provides a method to predict the median path loss for a telecommunication link. Developed on the basis of diffraction theory, this model predicts the path loss as a function of the height of path blockage and the First Fresnel zone for the transmission link.
The COST Hata model is a radio propagation model that extends the urban Hata model to cover a more elaborated range of frequencies. It is the most often cited of the COST 231 models, also called the Hata Model PCS Extension. This model is the combination of empirical and deterministic models for estimating path loss in an urban area over frequency range of 800 MHz to 2000 MHz.
Young model is a radio propagation model that was built on the data collected on New York City. It typically models the behaviour of cellular communication systems in large cities.
The Lee model for area-to-area mode is a radio propagation model that operates around 900 MHz. Built as two different modes, this model includes an adjustment factor that can be adjusted to make the model more flexible to different regions of propagation.
The ITU single vegetative obstruction model is a radio propagation model that quantitatively estimates attenuation due to a single plant or tree standing in the middle of a telecommunication link.
The Lee model for point-to-point mode is a radio propagation model that operates around 900 MHz. Built as two different modes, this model includes an adjustment factor that can be adjusted to make the model more flexible to different regions of propagation.
The log-distance path loss model is a radio propagation model that predicts the path loss a signal encounters inside a building or densely populated areas over distance.
The Hata model is a radio propagation model for predicting the path loss of cellular transmissions in exterior environments, valid for microwave frequencies from 150 to 1500 MHz. It is an empirical formulation based on the data from the Okumura model, and is thus also commonly referred to as the Okumura–Hata model. The model incorporates the graphical information from Okumura model and develops it further to realize the effects of diffraction, reflection and scattering caused by city structures. Additionally, the Hata Model applies corrections for applications in suburban and rural environments.
This is an index to articles about terms used in discussion of radio propagation.
The two-rays ground-reflection model is a multipath radio propagation model which predicts the path losses between a transmitting antenna and a receiving antenna when they are in line of sight (LOS). Generally, the two antenna each have different height. The received signal having two components, the LOS component and the reflection component formed predominantly by a single ground reflected wave.
In the domain of wireless communication, air-to-ground channels (A2G) are used for linking airborne devices, such as drones and aircraft, with terrestrial communication equipment. These channels are instrumental in a wide array of applications, extending beyond commercial telecommunications — including important roles in 5G and forthcoming 6G networks, where aerial base stations are integral to Non-Terrestrial Networks — to encompass critical uses in emergency response, environmental monitoring, military communications, and the expanding domain of the internet of things (IoT). A comprehensive understanding of A2G channels, their operational mechanics, and distinct attributes is essential for the enhancement of wireless network performance.
