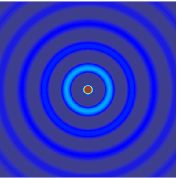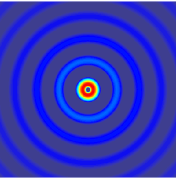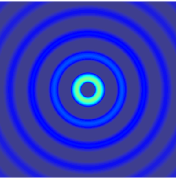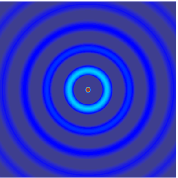
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves or electromagnetic waves. It arises in fields like acoustics, electromagnetism, and fluid dynamics.

In mathematics, Legendre polynomials, named after Adrien-Marie Legendre (1782), are a system of complete and orthogonal polynomials with a vast number of mathematical properties and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.
In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain differential equations. The idea is to write the solution of the differential equation as a sum of certain "basis functions" and then to choose the coefficients in the sum in order to satisfy the differential equation as well as possible.
In mathematics, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form:
In mathematics and its applications, a Sturm–Liouville problem is a second-order linear ordinary differential equation of the form:

In mathematics, the method of Frobenius, named after Ferdinand Georg Frobenius, is a way to find an infinite series solution for a linear second-order ordinary differential equation of the form
Harmonic balance is a method used to calculate the steady-state response of nonlinear differential equations, and is mostly applied to nonlinear electrical circuits. It is a frequency domain method for calculating the steady state, as opposed to the various time-domain steady-state methods. The name "harmonic balance" is descriptive of the method, which starts with Kirchhoff's Current Law written in the frequency domain and a chosen number of harmonics. A sinusoidal signal applied to a nonlinear component in a system will generate harmonics of the fundamental frequency. Effectively the method assumes a linear combination of sinusoids can represent the solution, then balances current and voltage sinusoids to satisfy Kirchhoff's law. The method is commonly used to simulate circuits which include nonlinear elements, and is most applicable to systems with feedback in which limit cycles occur.
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

In mathematics, the inverse scattering transform is a method that solves the initial value problem for a nonlinear partial differential equation using mathematical methods related to wave scattering. The direct scattering transform describes how a function scatters waves or generates bound-states. The inverse scattering transform uses wave scattering data to construct the function responsible for wave scattering. The direct and inverse scattering transforms are analogous to the direct and inverse Fourier transforms which are used to solve linear partial differential equations.
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation, Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.
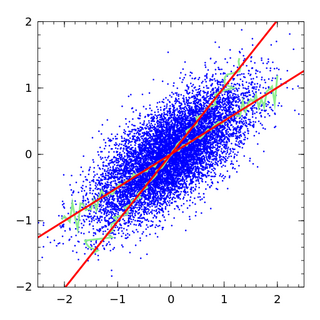
In statistics, errors-in-variables models or measurement error models are regression models that account for measurement errors in the independent variables. In contrast, standard regression models assume that those regressors have been measured exactly, or observed without error; as such, those models account only for errors in the dependent variables, or responses.
In mathematics, the Mittag-Leffler polynomials are the polynomials gn(x) or Mn(x) studied by Mittag-Leffler (1891).
In mathematics, a Ramanujan–Sato series generalizes Ramanujan’s pi formulas such as,
Mean-field particle methods are a broad class of interacting type Monte Carlo algorithms for simulating from a sequence of probability distributions satisfying a nonlinear evolution equation. These flows of probability measures can always be interpreted as the distributions of the random states of a Markov process whose transition probabilities depends on the distributions of the current random states. A natural way to simulate these sophisticated nonlinear Markov processes is to sample a large number of copies of the process, replacing in the evolution equation the unknown distributions of the random states by the sampled empirical measures. In contrast with traditional Monte Carlo and Markov chain Monte Carlo methods these mean-field particle techniques rely on sequential interacting samples. The terminology mean-field reflects the fact that each of the samples interacts with the empirical measures of the process. When the size of the system tends to infinity, these random empirical measures converge to the deterministic distribution of the random states of the nonlinear Markov chain, so that the statistical interaction between particles vanishes. In other words, starting with a chaotic configuration based on independent copies of initial state of the nonlinear Markov chain model, the chaos propagates at any time horizon as the size the system tends to infinity; that is, finite blocks of particles reduces to independent copies of the nonlinear Markov process. This result is called the propagation of chaos property. The terminology "propagation of chaos" originated with the work of Mark Kac in 1976 on a colliding mean-field kinetic gas model.
In fluid dynamics, a stagnation point flow refers to a fluid flow in the neighbourhood of a stagnation point or a stagnation line with which the stagnation point/line refers to a point/line where the velocity is zero in the inviscid approximation. The flow specifically considers a class of stagnation points known as saddle points wherein incoming streamlines gets deflected and directed outwards in a different direction; the streamline deflections are guided by separatrices. The flow in the neighborhood of the stagnation point or line can generally be described using potential flow theory, although viscous effects cannot be neglected if the stagnation point lies on a solid surface.
The Fuchsian theory of linear differential equations, which is named after Lazarus Immanuel Fuchs, provides a characterization of various types of singularities and the relations among them.
Tau functions are an important ingredient in the modern mathematical theory of integrable systems, and have numerous applications in a variety of other domains. They were originally introduced by Ryogo Hirota in his direct method approach to soliton equations, based on expressing them in an equivalent bilinear form.
Kapteyn series is a series expansion of analytic functions on a domain in terms of the Bessel function of the first kind. Kapteyn series are named after Willem Kapteyn, who first studied such series in 1893. Let be a function analytic on the domain


































