In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron. They have either skew regular faces or skew regular vertex figures.
In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron. They have either skew regular faces or skew regular vertex figures.
In 1926 John Flinders Petrie took the concept of a regular skew polygons, polygons whose vertices are not all in the same plane, and extended it to polyhedra. While apeirohedra are typically required to tile the 2-dimensional plane, Petrie considered cases where the faces were still convex but were not required to lie flat in the plane, they could have a skew polygon vertex figure.
Petrie discovered two regular skew apeirohedra, the mucube and the muoctahedron. [1] Harold Scott MacDonald Coxeter derived a third, the mutetrahedron, and proved that the these three were complete. Under Coxeter and Petrie's definition, requiring convex faces and allowing a skew vertex figure, the three were not only the only skew apeirohedra in 3-dimensional Euclidean space, but they were the only skew polyhedra in 3-space as there Coxeter showed there were no finite cases.
In 1967 [2] Garner investigated regular skew apeirohedra in hyperbolic 3-space with Petrie and Coxeters definition, discovering 31 [note 1] regular skew apeirohedra with compact or paracompact symmetry.
In 1977 [3] [1] Grünbaum generalized skew polyhedra to allow for skew faces as well. Grünbaum discovered an additional 23 [note 2] skew apeirohedra in 3-dimensional Euclidean space and 3 in 2-dimensional space which are skew by virtue of their faces. 12 of Grünbaum's polyhedra were formed using the blending operation on 2-dimensional apeirohedra, and the other 11 were pure, i.e. could not be formed by a non-trivial blend. Grünbaum conjectured that this new list was complete for the parameters considered.
In 1985 [4] [1] Dress found an additional pure regular skew apeirohedron in 3-space, and proved that with this additional skew apeirohedron the list was complete.
The three Euclidean solutions in 3-space are {4,6|4}, {6,4|4}, and {6,6|3}. John Conway named them mucube, muoctahedron, and mutetrahedron respectively for multiple cube, octahedron, and tetrahedron. [5]
Coxeter gives these regular skew apeirohedra {2q,2r|p} with extended chiral symmetry [[(p,q,p,r)]+] which he says is isomorphic to his abstract group (2q,2r|2,p). The related honeycomb has the extended symmetry [[(p,q,p,r)]]. [6]
| Coxeter group symmetry | Apeirohedron {p,q|l} | Image | Face {p} | Hole {l} | Vertex figure | Related honeycomb | |
|---|---|---|---|---|---|---|---|
   [[4,3,4]] [[4,3,4]+] | {4,6|4} Mucube |  animation |  | | 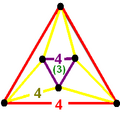 |  t0,3{4,3,4} |  |
| {6,4|4} Muoctahedron |  animation |  |  |  2t{4,3,4} |  | ||
 [[3[4]]] [[3[4]]+] | {6,6|3} Mutetrahedron |  animation | |  |  | q{4,3,4} |  |
There are 3 regular skew apeirohedra of full rank, also called regular skew honeycombs, that is skew apeirohedra in 2-dimensions. As with the finite skew polyhedra of full rank, all three of these can be obtained by applying the Petrie dual to planar polytopes, in this case the three regular tilings. [7] [8] [9]
Alternatively they can be constructed using the apeir operation on regular polygons. [10] While the Petrial is used the classical construction, it does not generalize well to higher ranks. In contrast, the apeir operation is used to construct higher rank skew honeycombs. [11]
The apeir operation takes the generating mirrors of the polygon, ρ0 and ρ1, and uses them as the mirrors for the vertex figure of a polyhedron, the new vertex mirror w is then a point located where the initial vertex of the polygon (or anywhere on the mirror ρ1 other than its intersection with ρ0). The new initial vertex is placed at the intersection of the mirrors ρ0 and ρ1. Thus the apeir polyhedron is generated by ⟨w, ρ0, ρ0⟩. [12]
| Skew honeycombs | Schläfli symbol | Faces | Image | Petrie dual | Apeir of | ||
|---|---|---|---|---|---|---|---|
| Petrial square tiling | {4,4}π | {∞,4}4 | ∞ zigzags |  | Square tiling | Square |  |
| Petrial triangular tiling | {3,6}π | {∞,6}3 | ∞ zigzags |  | Triangular tiling | Hexagon |  |
| Petrial hexagonal tiling | {6,3}π | {∞,3}6 | ∞ zigzags |  | Hexagonal tiling | Triangle |  |
For any two regular polytopes, P and Q, a new polytope can be made by the following process:
For regular polytopes the last step is guaranteed to produce a unique result. This new polytope is called the blend of P and Q and is represented P#Q.
Equivalently the blend can be obtained by positioning P and Q in orthogonal spaces and taking composing their generating mirrors pairwise.
Blended polyhedra in 3-dimensional space can be made by blending 2-dimensional polyhedra with 1-dimensional polytopes. The only 2-dimensional polyhedra are the 6 honeycombs (3 Euclidean tilings and 3 skew honeycombs):
The only 1-dimensional polytopes are:
Each pair between these produces a valid distinct regular skew apeirohedron in 3-dimensional Euclidean space, for a total of 12 [note 2] blended skew apeirohedra.
Since the skeleton of the square tiling is bipartite, two of these blends, {4, 4}#{} and {4, 4}π#{}, are combinatrially equivalent to their non-blended counterparts.
 | This section needs expansion. You can help by adding to it. (February 2024) |
A polytope is considered pure if it cannot be expressed as a non-trivial blend of two polytopes. A blend is considered trivial if it contains the result as one of the components. Alternatively a pure polytope is one whose symmetry group contains no non-trivial subrepresentation. [13]
There are 12 regular pure apeirohedra in 3 dimensions. Three of these are the Petrie-Coxeter polyhedra:
Three more are obtained as the Petrials of the Petrie-Coxeter polyhedra:
Three additional pure apeirohedra can be formed with finite skew polygons as faces:
These 3 are closed under the Wilson operations. Meaning that each can be constructed from any other by some combination of the Petrial and dual operations. {6,6}4 is self-dual and {6,4}6 is self-Petrial.
In 1967, C. W. L. Garner identified 31 hyperbolic skew apeirohedra with regular skew polygon vertex figures, found by extending the Petrie-Coxeter polyhedra to hyperbolic space. [14]
These represent 14 compact and 17 [note 1] paracompact regular skew polyhedra in hyperbolic space, constructed from the symmetry of a subset of linear and cyclic Coxeter groups graphs of the form [[(p,q,p,r)]], These define regular skew polyhedra {2q,2r|p} and dual {2r,2q|p}. For the special case of linear graph groups r = 2, this represents the Coxeter group [p,q,p]. It generates regular skews {2q,4|p} and {4,2q|p}. All of these exist as a subset of faces of the convex uniform honeycombs in hyperbolic space.
The skew apeirohedron shares the same antiprism vertex figure with the honeycomb, but only the zig-zag edge faces of the vertex figure are realized, while the other faces make holes.
| Coxeter group | Apeirohedron {p,q|l} | Face {p} | Hole {l} | Honeycomb | Vertex figure | Apeirohedron {p,q|l} | Face {p} | Hole {l} | Honeycomb | Vertex figure | |
|---|---|---|---|---|---|---|---|---|---|---|---|
 [3,5,3] | {10,4|3} | 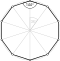 |  | 2t{3,5,3} | 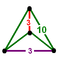 | {4,10|3} |  | | t0,3{3,5,3} |  | |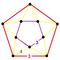
 [5,3,5] | {6,4|5} |  |  | 2t{5,3,5} | 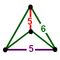 | {4,6|5} | | | t0,3{5,3,5} |  | |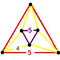
 [(4,3,3,3)] | {8,6|3} |  | | ct{(4,3,3,3)} | 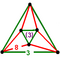 | {6,8|3} | | | ct{(3,3,4,3)} |  | |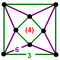
[(5,3,3,3)] | {10,6|3} | | | ct{(5,3,3,3)} | 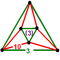 | {6,10|3} | | | ct{(3,3,5,3)} |  | |
[(4,3,4,3)] | {8,8|3} | | | ct{(4,3,4,3)} | 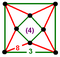 | {6,6|4} | | |   ct{(3,4,3,4)} |  | |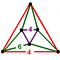
[(5,3,4,3)] | {8,10|3} | | | ct{(4,3,5,3)} | 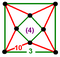 | {10,8|3} | | | ct{(5,3,4,3)} |  | |
[(5,3,5,3)] | {10,10|3} | | | ct{(5,3,5,3)} | 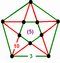 | {6,6|5} | | | ct{(3,5,3,5)} |  |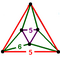
| Coxeter group | Apeirohedron {p,q|l} | Face {p} | Hole {l} | Honeycomb | Vertex figure | Apeirohedron {p,q|l} | Face {p} | Hole {l} | Honeycomb | Vertex figure | |
|---|---|---|---|---|---|---|---|---|---|---|---|
[4,4,4] | {8,4|4} | | | 2t{4,4,4} | 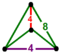 | {4,8|4} | | | t0,3{4,4,4} |  | |
 [3,6,3] | {12,4|3} | 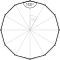 | | 2t{3,6,3} | 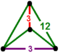 | {4,12|3} | | | t0,3{3,6,3} |  | |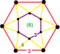
 [6,3,6] | {6,4|6} | | | 2t{6,3,6} |  | {4,6|6} | | | t0,3{6,3,6} |  | |
[(4,4,4,3)] | {8,6|4} | | | ct{(4,4,3,4)} |  | {6,8|4} | | | ct{(3,4,4,4)} |  | |
[(4,4,4,4)] | {8,8|4} | | | q{4,4,4} |  | ||||||
 [(6,3,3,3)] | {12,6|3} | | | ct{(6,3,3,3)} | 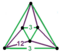 | {6,12|3} | | | ct{(3,3,6,3)} |  | |
[(6,3,4,3)] | {12,8|3} | | | ct{(6,3,4,3)} | 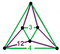 | {8,12|3} | | | ct{(4,3,6,3)} | | |
[(6,3,5,3)] | {12,10|3} | | | ct{(6,3,5,3)} |  | {10,12|3} | | | ct{(5,3,6,3)} |  | |
[(6,3,6,3)] | {12,12|3} | | | ct{(6,3,6,3)} | 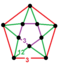 | {6,6|6} | | | ct{(3,6,3,6)} |  |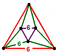
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.
In elementary geometry, a polytope is a geometric object with flat sides (faces). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a (k + 1)-polytope consist of k-polytopes that may have (k – 1)-polytopes in common.
In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .
In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.
The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.
In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.
In geometry, an apeirogon or infinite polygon is a polygon with an infinite number of sides. Apeirogons are the rank 2 case of infinite polytopes. In some literature, the term "apeirogon" may refer only to the regular apeirogon, with an infinite dihedral group of symmetries.
In geometry, a skew polygon is a polygon whose vertices are not all coplanar. Skew polygons must have at least four vertices. The interior surface of such a polygon is not uniquely defined.
In geometry, a skew apeirohedron is an infinite skew polyhedron consisting of nonplanar faces or nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface.
In geometry, an apeirotope or infinite polytope is a generalized polytope which has infinitely many facets.
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon in which every n – 1 consecutive sides belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie.
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedra which include the possibility of nonplanar faces or vertex figures. Coxeter looked at skew vertex figures which created new 4-dimensional regular polyhedra, and much later Branko Grünbaum looked at regular skew faces.
In hyperbolic geometry, a uniform honeycomb in hyperbolic space is a uniform tessellation of uniform polyhedral cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by permutations of rings of the Coxeter diagrams for each family.
In geometry, the order-4 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {6,4}.