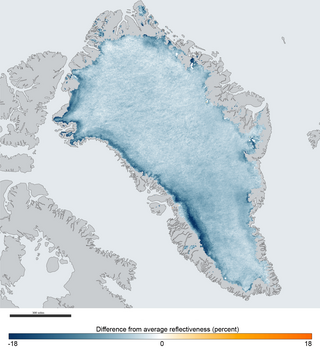
Albedo is the fraction of sunlight that is diffusely reflected by a body. It is measured on a scale from 0 to 1. Surface albedo is defined as the ratio of radiosity Je to the irradiance Ee received by a surface. The proportion reflected is not only determined by properties of the surface itself, but also by the spectral and angular distribution of solar radiation reaching the Earth's surface. These factors vary with atmospheric composition, geographic location, and time.
In astronomy, absolute magnitude is a measure of the luminosity of a celestial object on an inverse logarithmic astronomical magnitude scale. An object's absolute magnitude is defined to be equal to the apparent magnitude that the object would have if it were viewed from a distance of exactly 10 parsecs, without extinction of its light due to absorption by interstellar matter and cosmic dust. By hypothetically placing all objects at a standard reference distance from the observer, their luminosities can be directly compared among each other on a magnitude scale. For Solar System bodies that shine in reflected light, a different definition of absolute magnitude (H) is used, based on a standard reference distance of one astronomical unit.

Mathilde is an asteroid in the intermediate asteroid belt, approximately 50 kilometers in diameter, that was discovered by Austrian astronomer Johann Palisa at Vienna Observatory on 12 November 1885. It has a relatively elliptical orbit that requires more than four years to circle the Sun. This tumbling asteroid has an unusually slow rate of rotation, requiring 17.4 days to complete a 360° revolution about its axis. It is a primitive C-type asteroid, which means the surface has a high proportion of carbon; giving it a dark surface that reflects only 4% of the light that falls on it.

In fluid mechanics, hydrostatic equilibrium is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space. In general, it is what causes objects in space to be spherical.
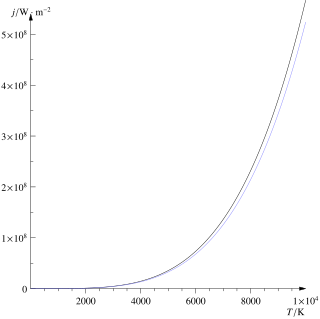
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.
The orbital period is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.

The Hill sphere is a common model for the calculation of a gravitational sphere of influence. It is the most commonly used model to calculate the spatial extent of gravitational influence of an astronomical body (m) in which it dominates over the gravitational influence of other bodies, particularly a primary (M). It is sometimes confused with other models of gravitational influence, such as the Laplace sphere or being called the Roche sphere, the latter causing confusion with the Roche limit. It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche.

Orbital decay is a gradual decrease of the distance between two orbiting bodies at their closest approach over many orbital periods. These orbiting bodies can be a planet and its satellite, a star and any object orbiting it, or components of any binary system. If left unchecked, the decay eventually results in termination of the orbit when the smaller object strikes the surface of the primary; or for objects where the primary has an atmosphere, the smaller object burns, explodes, or otherwise breaks up in the larger object's atmosphere; or for objects where the primary is a star, ends with incineration by the star's radiation. Collisions of stellar-mass objects are usually accompanied by effects such as gamma-ray bursts and detectable gravitational waves.

Black-body radiation is the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body. It has a specific, continuous spectrum of wavelengths, inversely related to intensity, that depend only on the body's temperature, which is assumed, for the sake of calculations and theory, to be uniform and constant.
In celestial mechanics, the standard gravitational parameterμ of a celestial body is the product of the gravitational constant G and the total mass M of the bodies. For two bodies, the parameter may be expressed as G(m1 + m2), or as GM when one body is much larger than the other:
The effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation. Effective temperature is often used as an estimate of a body's surface temperature when the body's emissivity curve is not known.

Eukrate is a rather large main-belt asteroid. It is dark and probably a primitive carbonaceous body. The asteroid was discovered by Robert Luther on March 14, 1885, in Düsseldorf. It was named after Eucrate, a Nereid in Greek mythology.
In orbital mechanics, mean motion is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass. While nominally a mean, and theoretically so in the case of two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above conditions as calculated from the current gravitational and geometric circumstances of the body's constantly-changing, perturbed orbit.
794 Irenaea is a dark background asteroid from the outer regions of the asteroid belt. It was discovered on 27 August 1914, by Austrian astronomer Johann Palisa at the Vienna Observatory. The presumed C-type asteroid has a rotation period of 9.1 hours and measures approximately 36 kilometers in diameter. It was likely named after Irene Hillebrand, daughter of Austrian astronomer Edmund Weiss (1837–1917).
"Clearing the neighbourhood" around a celestial body's orbit describes the body becoming gravitationally dominant such that there are no other bodies of comparable size other than its natural satellites or those otherwise under its gravitational influence.
The two-body problem in general relativity is the determination of the motion and gravitational field of two bodies as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet orbiting its sun. Solutions are also used to describe the motion of binary stars around each other, and estimate their gradual loss of energy through gravitational radiation.
16560 Daitor (; provisional designation 1991 VZ5) is a large Jupiter trojan from the Trojan camp, approximately 44 kilometers (27 miles) in diameter. It was discovered on 2 November 1991, by Belgian astronomer Eric Elst at the La Silla site of the European Southern Observatory in Chile. The carbonaceous C-type asteroid is one of the largest Jupiter trojans with an unknown rotation period. It was named after the Trojan warrior Daitor from Greek mythology.
The planetary equilibrium temperature is a theoretical temperature that a planet would be if it were in radiative equilibrium, typically under the assumption that it radiates as a black body being heated only by its parent star. In this model, the presence or absence of an atmosphere is irrelevant, as the equilibrium temperature is calculated purely from a balance with incident stellar energy.
(31345) 1998 PG is an eccentric, stony asteroid and binary system, classified as near-Earth object of the Amor group of asteroids, approximately 900 meters in diameter. It minor-planet moon, S/2001 (31345) 1, has an estimated diameter of 270 meters.
In Einstein's theory of general relativity, the interior Schwarzschild metric is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric.



















































