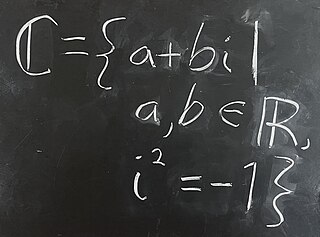Table of mathematical symbols by introduction date

Last updated February 27, 2024

This article contains Unicode mathematical symbols. Without proper rendering support, you may see question marks, boxes, or other symbols instead of mathematical symbols.

The following table lists many specialized symbols commonly used in modern mathematics, ordered by their introduction date. The table can also be ordered alphabetically by clicking on the relevant header title.

Symbol	Name	Date of earliest use	First author to use
—	horizontal bar for division	14th century (approx.)	Nicole Oresme ^[1]
+	plus sign	1360 (approx.), abbreviation for Latin et resembling the plus sign	Nicole Oresme
−	minus sign	1489 (first appearance of minus sign, and also first appearance of plus sign in print)	Johannes Widmann
√	radical symbol (for square root)	1525 (without the vinculum above the radicand)	Christoff Rudolff
(...)	parentheses (for precedence grouping)	1544 (in handwritten notes)	Michael Stifel
(...)	parentheses (for precedence grouping)	1556	Niccolò Tartaglia
=	equals sign	1557	Robert Recorde
.	decimal separator	1593	Christopher Clavius
×	multiplication sign	1618	William Oughtred
±	plus–minus sign	1628
∷	proportion sign	1628
ⁿ√	radical symbol (for nth root)	1629	Albert Girard
< >	strict inequality signs (less-than sign and greater-than sign)	1631	Thomas Harriot
x^y	superscript notation (for exponentiation)	1636 (using Roman numerals as superscripts)	James Hume
x^y	superscript notation (for exponentiation)	1637 (in the modern form)	René Descartes (La Géométrie)
x	Use of the letter x for an independent variable or unknown value. See History of algebra: The symbol x.	1637^[2]	René Descartes (La Géométrie)
√ ̅	radical symbol (for square root)	1637 (with the vinculum above the radicand)	René Descartes (La Géométrie)
%	percent sign	1650 (approx.)	unknown
∞	infinity sign	1655	John Wallis
÷	division sign (a repurposed obelus variant)	1659	Johann Rahn
≤ ≥	unstrict inequality signs (less-than or equals to sign and greater-than or equals to sign)	1670 (with the horizontal bar over the inequality sign, rather than below it)	John Wallis
≤ ≥		1734 (with double horizontal bar below the inequality sign)	Pierre Bouguer
d	differential sign	1675	Gottfried Leibniz
∫	integral sign	1675
:	colon (for division)	1684 (deriving from use of colon to denote fractions, dating back to 1633)
·	middle dot (for multiplication)	1698 (perhaps deriving from a much earlier use of middle dot to separate juxtaposed numbers)
⁄	division slash (a.k.a. solidus)	1718 (deriving from horizontal fraction bar, invented by Abu Bakr al-Hassar in the 12th century)	Thomas Twining
≠	inequality sign (not equal to)	unknown	Leonhard Euler
x′	prime symbol (for derivative)	1748
Σ	summation symbol	1755
∝	proportionality sign	1768	William Emerson
∂	partial differential sign (a.k.a. curly d or Jacobi's delta)	1770	Marquis de Condorcet
≡	identity sign (for congruence relation)	1801 (first appearance in print; used previously in personal writings of Gauss)	Carl Friedrich Gauss
[x]	integral part (a.k.a. floor)	1808	Carl Friedrich Gauss
!	factorial	1808	Christian Kramp
Π	product symbol	1812	Carl Friedrich Gauss
⊂ ⊃	set inclusion signs (subset of, superset of)	1817	Joseph Gergonne
⊂ ⊃	set inclusion signs (subset of, superset of)	1890	Ernst Schröder
\|...\|	absolute value notation	1841	Karl Weierstrass
\|...\|	determinant of a matrix	1841	Arthur Cayley
‖...‖	matrix notation	1843^[3]	Arthur Cayley
∇	nabla symbol (for vector differential)	1846 (previously used by Hamilton as a general-purpose operator sign)	William Rowan Hamilton
∩ ∪	intersection union	1888	Giuseppe Peano
ℵ	aleph symbol (for transfinite cardinal numbers)	1893	Georg Cantor
∈	membership sign (is an element of)	1894	Giuseppe Peano
O	Big O Notation	1894	Paul Bachmann
{...}	braces, a.k.a. curly brackets (for set notation)	1895	Georg Cantor
$\mathbb {N}$	Blackboard bold capital N (for natural numbers set)	1895	Giuseppe Peano
$\mathbb {Q}$	Blackboard bold capital Q (for rational numbers set)	1895
∃	existential quantifier (there exists)	1897
·	middle dot (for dot product)	1902	J. Willard Gibbs
×	multiplication sign (for cross product)	1902	J. Willard Gibbs
∨	logical disjunction (a.k.a. OR)	1906	Bertrand Russell
(...)	matrix notation	1909^[3]	Maxime Bôcher
[...]	matrix notation	1909^[3]	Gerhard Kowalewski
∮	contour integral sign	1917	Arnold Sommerfeld
$\mathbb {Z}$	Blackboard bold capital Z (for integer numbers set)	1930	Edmund Landau
∀	universal quantifier (for all)	1935	Gerhard Gentzen
→	arrow (for function notation)	1936 (to denote images of specific elements)	Øystein Ore
→	arrow (for function notation)	1940 (in the present form of f: X → Y)	Witold Hurewicz
∅	empty set sign	1939	André Weil / Nicolas Bourbaki ^[4]
$\mathbb {C}$	Blackboard bold capital C (for complex numbers set)	1939	Nathan Jacobson
∎	end of proof sign (a.k.a. tombstone)	1950^[5]	Paul Halmos
⌊x⌋ ⌈x⌉	greatest integer ≤ x (a.k.a. floor) smallest integer ≥ x (a.k.a. ceiling)	1962^[6]	Kenneth E. Iverson

Sources

↑ Cajori, Florian (1993). A History of Mathematical Notations. Mineola, New York: Dover Publications.
↑ Boyer, Carl B. (1991), A History of Mathematics (Second ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8
1 2 3 "Earliest Uses of Symbols for Matrices and Vectors". jeff560.tripod.com. Retrieved 18 December 2016.
↑ Weil, André (1992), The Apprenticeship of a Mathematician, Springer, p. 114, ISBN 9783764326500 .
↑ Halmos, Paul (1950). Measure Theory. New York: Van Nostrand. pp. vi. The symbol ∎ is used throughout the entire book in place of such phrases as "Q.E.D." or "This completes the proof of the theorem" to signal the end of a proof.
↑ Kenneth E. Iverson (1962), A Programming Language, Wiley, retrieved 20 April 2016

External links

Related Research Articles

Q.E.D. or QED is an initialism of the Latin phrase quod erat demonstrandum, meaning "that which was to be demonstrated". Literally it states "what was to be shown". Traditionally, the abbreviation is placed at the end of mathematical proofs and philosophical arguments in print publications, to indicate that the proof or the argument is complete.

0 (zero) is a number representing an empty quantity. Adding 0 to any number leaves that number unchanged. In mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and complex numbers, as well as other algebraic structures. Multiplying any number by 0 has the result 0, and consequently, division by zero has no meaning in arithmetic.

Blackboard bold is a style of writing bold symbols on a blackboard by doubling certain strokes, commonly used in mathematical lectures, and the derived style of typeface used in printed mathematical texts. The style is most commonly used to represent the number sets $, (integers),,, and .$

A bracket is either of two tall fore- or back-facing punctuation marks commonly used to isolate a segment of text or data from its surroundings. They come in four main pairs of shapes, as given in the box to the right, which also gives their names, that vary between British and American English. "Brackets", without further qualification, are in British English the (…) marks and in American English the […] marks.

The multiplication sign, also known as the times sign or the dimension sign, is a mathematical symbol used to denote the operation of multiplication, which results in a product. While similar to a lowercase X, the form is properly a four-fold rotationally symmetric saltire.

The division sign is a mathematical symbol consisting of a short horizontal line with a dot above and another dot below, used in Anglophone countries to indicate the operation of division. This usage, though widespread in some countries, is not universal and the symbol has a different meaning in other countries. Its use to denote division is not recommended in the ISO 80000-2 standard for mathematical notation.

Mathematical notation consists of using symbols for representing operations, unspecified numbers, relations, and any other mathematical objects and assembling them into expressions and formulas. Mathematical notation is widely used in mathematics, science, and engineering for representing complex concepts and properties in a concise, unambiguous, and accurate way.

The equals sign or equal sign, also known as the equality sign, is the mathematical symbol =, which is used to indicate equality in some well-defined sense. In an equation, it is placed between two expressions that have the same value, or for which one studies the conditions under which they have the same value.

The prime symbol ′, double prime symbol ″, triple prime symbol ‴, and quadruple prime symbol ⁗ are used to designate units and for other purposes in mathematics, science, linguistics and music.

<span class="mw-page-title-main">Tombstone (typography)</span> Symbol used in mathematics and typography

In mathematics, the tombstone, halmos, end-of-proof, or Q.E.D. symbol "∎" is a symbol used to denote the end of a proof, in place of the traditional abbreviation "Q.E.D." for the Latin phrase "quod erat demonstrandum". It is inspired by the typographic practice of end marks, an element that marks the end of an article.

The degree symbol or degree sign, °, is a glyph or symbol that is used, among other things, to represent degrees of arc, hours, degrees of temperature or alcohol proof. The symbol consists of a small superscript circle.

The infinity symbol is a mathematical symbol representing the concept of infinity. This symbol is also called a lemniscate, after the lemniscate curves of a similar shape studied in algebraic geometry, or "lazy eight", in the terminology of livestock branding.

The integral symbol:

In logical argument and mathematical proof, the therefore sign, ∴, is generally used before a logical consequence, such as the conclusion of a syllogism. The symbol consists of three dots placed in an upright triangle and is read therefore. While it is not generally used in formal writing, it is used in mathematics and shorthand.

Turned A is a letter and symbol based upon the letter A.

Mathematics is a field of study that investigates topics such as number, space, structure, and change.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Cajori, Florian (1993). A History of Mathematical Notations. Mineola, New York: Dover Publications.

[2] Boyer, Carl B. (1991), A History of Mathematics (Second ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8

[matrix-3] 1 2 3 "Earliest Uses of Symbols for Matrices and Vectors". jeff560.tripod.com. Retrieved 18 December 2016.

[4] Weil, André (1992), The Apprenticeship of a Mathematician, Springer, p. 114, ISBN 9783764326500 .

[5] Halmos, Paul (1950). Measure Theory. New York: Van Nostrand. pp. vi. The symbol ∎ is used throughout the entire book in place of such phrases as "Q.E.D." or "This completes the proof of the theorem" to signal the end of a proof.

[6] Kenneth E. Iverson (1962), A Programming Language, Wiley, retrieved 20 April 2016

[1]

[2]

[3]

[4]

[5]

[6]

Table of mathematical symbols by introduction date

Contents

See also

Sources

External links

Related Research Articles