In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to a straight line segment.
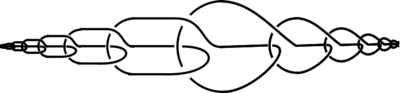
Antoine (1920) found the first example of a wild arc. Fox & Artin (1948) found another example, called the Fox-Artin arc, whose complement is not simply connected.
Two very similar wild arcs appear in the Fox & Artin (1948) article. Example 1.1 (page 981) is most generally referred to as the Fox-Artin wild arc. The crossings have the regular sequence over/over/under/over/under/under when following the curve from left to right.
The left end-point 0 of the closed unit interval is mapped by the arc to the left limit point of the curve, and 1 is mapped to the right limit point. The range of the arc lies in the Euclidean space or the 3-sphere .
Example 1.1* has the crossing sequence over/under/over/under/over/under. According to Fox & Artin (1948), page 982: "This is just the chain stitch of knitting extended indefinitely in both directions."
This arc cannot be continuously deformed to produce Example 1.1 in or , despite its similar appearance.
Also shown here is an alternative style of diagram for the arc in Example 1.1*.
| Fields |  | |
|---|---|---|
| Key concepts | ||
| Metrics and properties | ||
| Key results | ||
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces.
In mathematics, differential topology is the field dealing with the topological properties and smooth properties of smooth manifolds. In this sense differential topology is distinct from the closely related field of differential geometry, which concerns the geometric properties of smooth manifolds, including notions of size, distance, and rigid shape. By comparison differential topology is concerned with coarser properties, such as the number of holes in a manifold, its homotopy type, or the structure of its diffeomorphism group. Because many of these coarser properties may be captured algebraically, differential topology has strong links to algebraic topology.
In mathematics and more specifically in topology, a homeomorphism, also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.
In mathematics, a (real) interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite.
In mathematics, a curve is an object similar to a line, but that does not have to be straight.
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself.
In mathematical analysis, a space-filling curve is a curve whose range reaches every point in a higher dimensional region, typically the unit square. Because Giuseppe Peano (1858–1932) was the first to discover one, space-filling curves in the 2-dimensional plane are sometimes called Peano curves, but that phrase also refers to the Peano curve, the specific example of a space-filling curve found by Peano.
In mathematics, and specifically in topology, a CW complex is a topological space that is built by gluing together topological balls of different dimensions in specific ways. It generalizes both manifolds and simplicial complexes and has particular significance for algebraic topology. It was initially introduced by J. H. C. Whitehead to meet the needs of homotopy theory. CW complexes have better categorical properties than simplicial complexes, but still retains a combinatorial nature that allows for computation.
In mathematics, specifically algebraic geometry, a scheme is a structure that enlarges the notion of algebraic variety in several ways, such as taking account of multiplicities and allowing "varieties" defined over any commutative ring.
The Alexander horned sphere is a pathological object in topology discovered by J. W. Alexander. It is a particular topological embedding of a two-dimensional sphere in three-dimensional space. Together with its inside, it is a topological 3-ball, the Alexander horned ball, and so is simply connected; i.e., every loop can be shrunk to a point while staying inside. However, the exterior is not simply connected, unlike the exterior of the usual round sphere.
In mathematics, the Hawaiian earring is the topological space defined by the union of circles in the Euclidean plane with center and radius for endowed with the subspace topology:
In mathematics, the Teichmüller space of a (real) topological surface is a space that parametrizes complex structures on up to the action of homeomorphisms that are isotopic to the identity homeomorphism. Teichmüller spaces are named after Oswald Teichmüller.
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.
In mathematics, an exotic is a differentiable manifold that is homeomorphic but not diffeomorphic to the Euclidean space The first examples were found in 1982 by Michael Freedman and others, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's theorems about smooth 4-manifolds. There is a continuum of non-diffeomorphic differentiable structures as was shown first by Clifford Taubes.
In mathematics, an immersion is a differentiable function between differentiable manifolds whose differential pushforward is everywhere injective. Explicitly, f : M → N is an immersion if
In mathematics a stack or 2-sheaf is, roughly speaking, a sheaf that takes values in categories rather than sets. Stacks are used to formalise some of the main constructions of descent theory, and to construct fine moduli stacks when fine moduli spaces do not exist.
An infinite-dimensional vector function is a function whose values lie in an infinite-dimensional topological vector space, such as a Hilbert space or a Banach space.
In mathematics, the Thurston boundary of Teichmüller space of a surface is obtained as the boundary of its closure in the projective space of functionals on simple closed curves on the surface. The Thurston boundary can be interpreted as the space of projective measured foliations on the surface.
In mathematics, a configuration space is a construction closely related to state spaces or phase spaces in physics. In physics, these are used to describe the state of a whole system as a single point in a high-dimensional space. In mathematics, they are used to describe assignments of a collection of points to positions in a topological space. More specifically, configuration spaces in mathematics are particular examples of configuration spaces in physics in the particular case of several non-colliding particles.
