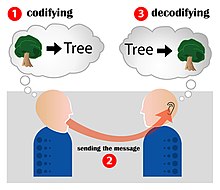
Computing is any goal-oriented activity requiring, benefiting from, or creating computing machinery. It includes the study and experimentation of algorithmic processes, and development of both hardware and software. Computing has scientific, engineering, mathematical, technological and social aspects. Major computing disciplines include computer engineering, computer science, cybersecurity, data science, information systems, information technology, digital art and software engineering.

A quantum computer is a computer that exploits quantum mechanical phenomena. At small scales, physical matter exhibits properties of both particles and waves, and quantum computing leverages this behavior, specifically quantum superposition and entanglement, using specialized hardware that supports the preparation and manipulation of quantum states. Classical physics cannot explain the operation of these quantum devices, and a scalable quantum computer could perform some calculations exponentially faster than any modern "classical" computer. In particular, a large-scale quantum computer could break widely used encryption schemes and aid physicists in performing physical simulations; however, the current state of the art is largely experimental and impractical, with several obstacles to useful applications.

Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information refers to both the technical definition in terms of Von Neumann entropy and the general computational term.

A wireless network is a computer network that uses wireless data connections between network nodes. Wireless networking allows homes, telecommunications networks and business installations to avoid the costly process of introducing cables into a building, or as a connection between various equipment locations. Admin telecommunications networks are generally implemented and administered using radio communication. This implementation takes place at the physical level (layer) of the OSI model network structure.
Quantum key distribution (QKD) is a secure communication method that implements a cryptographic protocol involving components of quantum mechanics. It enables two parties to produce a shared random secret key known only to them, which then can be used to encrypt and decrypt messages. The process of quantum key distribution is not to be confused with quantum cryptography, as it is the best-known example of a quantum-cryptographic task.

Photonics is a branch of optics that involves the application of generation, detection, and manipulation of light in form of photons through emission, transmission, modulation, signal processing, switching, amplification, and sensing. Photonics is closely related to quantum electronics, where quantum electronics deals with the theoretical part of it while photonics deal with its engineering applications. Though covering all light's technical applications over the whole spectrum, most photonic applications are in the range of visible and near-infrared light. The term photonics developed as an outgrowth of the first practical semiconductor light emitters invented in the early 1960s and optical fibers developed in the 1970s.

Wireless communication is the transfer of information (telecommunication) between two or more points without the use of an electrical conductor, optical fiber or other continuous guided medium for the transfer. The most common wireless technologies use radio waves. With radio waves, intended distances can be short, such as a few meters for Bluetooth or as far as millions of kilometers for deep-space radio communications. It encompasses various types of fixed, mobile, and portable applications, including two-way radios, cellular telephones, personal digital assistants (PDAs), and wireless networking. Other examples of applications of radio wireless technology include GPS units, garage door openers, wireless computer mouse, keyboards and headsets, headphones, radio receivers, satellite television, broadcast television and cordless telephones. Somewhat less common methods of achieving wireless communications involve other electromagnetic phenomena, such as light and magnetic or electric fields, or the use of sound.
This is a timeline of quantum computing.

A mobile device is a computer, small enough to hold and operate in the hand. Mobile devices typically have a flat LCD or OLED screen, a touchscreen interface, and digital or physical buttons. They may also have a physical keyboard. Many such devices can connect to the Internet and connect with other devices such as car entertainment systems or headsets via Wi-Fi, Bluetooth, cellular networks or near field communication. Integrated cameras, the ability to place and receive voice and video telephone calls, video games, and Global Positioning System (GPS) capabilities are common. Power is typically provided by a lithium-ion battery. Mobile devices may run mobile operating systems that allow third-party applications to be installed and run.
Information and communications technology (ICT) is an extensional term for information technology (IT) that stresses the role of unified communications and the integration of telecommunications and computers, as well as necessary enterprise software, middleware, storage and audiovisual, that enable users to access, store, transmit, understand and manipulate information.
Quantum networks form an important element of quantum computing and quantum communication systems. Quantum networks facilitate the transmission of information in the form of quantum bits, also called qubits, between physically separated quantum processors. A quantum processor is a small quantum computer being able to perform quantum logic gates on a certain number of qubits. Quantum networks work in a similar way to classical networks. The main difference is that quantum networking, like quantum computing, is better at solving certain problems, such as modeling quantum systems.

Naturally occurring lanthanum (57La) is composed of one stable (139La) and one radioactive (138La) isotope, with the stable isotope, 139La, being the most abundant (99.91% natural abundance). There are 39 radioisotopes that have been characterized, with the most stable being 138La, with a half-life of 1.02×1011 years; 137La, with a half-life of 60,000 years and 140La, with a half-life of 1.6781 days. The remaining radioactive isotopes have half-lives that are less than a day and the majority of these have half-lives that are less than 1 minute. This element also has 12 nuclear isomers, the longest-lived of which is 132mLa, with a half-life of 24.3 minutes.

Quantum neural networks are computational neural network models which are based on the principles of quantum mechanics. The first ideas on quantum neural computation were published independently in 1995 by Subhash Kak and Ron Chrisley, engaging with the theory of quantum mind, which posits that quantum effects play a role in cognitive function. However, typical research in quantum neural networks involves combining classical artificial neural network models with the advantages of quantum information in order to develop more efficient algorithms. One important motivation for these investigations is the difficulty to train classical neural networks, especially in big data applications. The hope is that features of quantum computing such as quantum parallelism or the effects of interference and entanglement can be used as resources. Since the technological implementation of a quantum computer is still in a premature stage, such quantum neural network models are mostly theoretical proposals that await their full implementation in physical experiments.
Unconventional computing is computing by any of a wide range of new or unusual methods. It is also known as alternative computing.
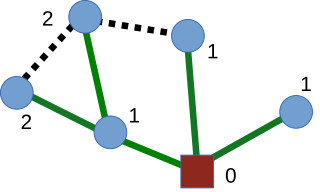
In mathematics and computer science, a shortest-path tree rooted at a vertex v of a connected, undirected graph G is a spanning tree T of G, such that the path distance from root v to any other vertex u in T is the shortest path distance from v to u in G.
Reservoir computing is a framework for computation derived from recurrent neural network theory that maps input signals into higher dimensional computational spaces through the dynamics of a fixed, non-linear system called a reservoir. After the input signal is fed into the reservoir, which is treated as a "black box," a simple readout mechanism is trained to read the state of the reservoir and map it to the desired output. The first key benefit of this framework is that training is performed only at the readout stage, as the reservoir dynamics are fixed. The second is that the computational power of naturally available systems, both classical and quantum mechanical, can be used to reduce the effective computational cost.
Quantum cryptography is the science of exploiting quantum mechanical properties to perform cryptographic tasks. The best known example of quantum cryptography is quantum key distribution which offers an information-theoretically secure solution to the key exchange problem. The advantage of quantum cryptography lies in the fact that it allows the completion of various cryptographic tasks that are proven or conjectured to be impossible using only classical communication. For example, it is impossible to copy data encoded in a quantum state. If one attempts to read the encoded data, the quantum state will be changed due to wave function collapse. This could be used to detect eavesdropping in quantum key distribution (QKD).

Quantum machine learning is the integration of quantum algorithms within machine learning programs. The most common use of the term refers to machine learning algorithms for the analysis of classical data executed on a quantum computer, i.e. quantum-enhanced machine learning. While machine learning algorithms are used to compute immense quantities of data, quantum machine learning utilizes qubits and quantum operations or specialized quantum systems to improve computational speed and data storage done by algorithms in a program. This includes hybrid methods that involve both classical and quantum processing, where computationally difficult subroutines are outsourced to a quantum device. These routines can be more complex in nature and executed faster on a quantum computer. Furthermore, quantum algorithms can be used to analyze quantum states instead of classical data. Beyond quantum computing, the term "quantum machine learning" is also associated with classical machine learning methods applied to data generated from quantum experiments, such as learning the phase transitions of a quantum system or creating new quantum experiments. Quantum machine learning also extends to a branch of research that explores methodological and structural similarities between certain physical systems and learning systems, in particular neural networks. For example, some mathematical and numerical techniques from quantum physics are applicable to classical deep learning and vice versa. Furthermore, researchers investigate more abstract notions of learning theory with respect to quantum information, sometimes referred to as "quantum learning theory".
In quantum computing, quantum memory is the quantum-mechanical version of ordinary computer memory. Whereas ordinary memory stores information as binary states, quantum memory stores a quantum state for later retrieval. These states hold useful computational information known as qubits. Unlike the classical memory of everyday computers, the states stored in quantum memory can be in a quantum superposition, giving much more practical flexibility in quantum algorithms than classical information storage.

Branched flow refers to a phenomenon in wave dynamics, that produces a tree-like pattern involving successive mostly forward scattering events by smooth obstacles deflecting traveling rays or waves. Sudden and significant momentum or wavevector changes are absent, but accumulated small changes can lead to large momentum changes. The path of a single ray is less important than the environs around a ray, which rotate, compress, and stretch around in an area preserving way. Even more revealing are groups, or manifolds of neighboring rays extending over significant zones. Starting rays out from a point but varying their direction over a range, one to the next, or from different points along a line all with the same initial directions are examples of a manifold. Waves have analogous launching conditions, such as a point source spraying in many directions, or an extended plane wave heading on one direction. The ray bending or refraction leads to characteristic structure in phase space and nonuniform distributions in coordinate space that look somehow universal and resemble branches in trees or stream beds. The branches taken on non-obvious paths through the refracting landscape that are indirect and nonlocal results of terrain already traversed. For a given refracting landscape, the branches will look completely different depending on the initial manifold.