Related Research Articles

A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimensions, a dihedral angle represents the angle between two hyperplanes. The planes of a flying machine are said to be at positive dihedral angle when both starboard and port main planes are upwardly inclined to the lateral axis; when downwardly inclined they are said to be at a negative dihedral angle.

In chemistry, polarity is a separation of electric charge leading to a molecule or its chemical groups having an electric dipole moment, with a negatively charged end and a positively charged end.
In computational chemistry and molecular physics, Gaussian orbitals are functions used as atomic orbitals in the LCAO method for the representation of electron orbitals in molecules and numerous properties that depend on these.

A chemical structure of a molecule is a spatial arrangement of its atoms and their chemical bonds. Its determination includes a chemist's specifying the molecular geometry and, when feasible and necessary, the electronic structure of the target molecule or other solid. Molecular geometry refers to the spatial arrangement of atoms in a molecule and the chemical bonds that hold the atoms together and can be represented using structural formulae and by molecular models; complete electronic structure descriptions include specifying the occupation of a molecule's molecular orbitals. Structure determination can be applied to a range of targets from very simple molecules to very complex ones.

Molecular modelling encompasses all methods, theoretical and computational, used to model or mimic the behaviour of molecules. The methods are used in the fields of computational chemistry, drug design, computational biology and materials science to study molecular systems ranging from small chemical systems to large biological molecules and material assemblies. The simplest calculations can be performed by hand, but inevitably computers are required to perform molecular modelling of any reasonably sized system. The common feature of molecular modelling methods is the atomistic level description of the molecular systems. This may include treating atoms as the smallest individual unit, or explicitly modelling protons and neutrons with its quarks, anti-quarks and gluons and electrons with its photons.

Molecular geometry is the three-dimensional arrangement of the atoms that constitute a molecule. It includes the general shape of the molecule as well as bond lengths, bond angles, torsional angles and any other geometrical parameters that determine the position of each atom.

In chemistry, sigma bonds are the strongest type of covalent chemical bond. They are formed by head-on overlapping between atomic orbitals. Sigma bonding is most simply defined for diatomic molecules using the language and tools of symmetry groups. In this formal approach, a σ-bond is symmetrical with respect to rotation about the bond axis. By this definition, common forms of sigma bonds are s+s, pz+pz, s+pz and dz2+dz2 . Quantum theory also indicates that molecular orbitals (MO) of identical symmetry actually mix or hybridize. As a practical consequence of this mixing of diatomic molecules, the wavefunctions s+s and pz+pz molecular orbitals become blended. The extent of this mixing depends on the relative energies of the MOs of like symmetry.
In chemistry, orbital hybridisation is the concept of mixing atomic orbitals to form new hybrid orbitals suitable for the pairing of electrons to form chemical bonds in valence bond theory. For example, in a carbon atom which forms four single bonds the valence-shell s orbital combines with three valence-shell p orbitals to form four equivalent sp3 mixtures in a tetrahedral arrangement around the carbon to bond to four different atoms. Hybrid orbitals are useful in the explanation of molecular geometry and atomic bonding properties and are symmetrically disposed in space. Usually hybrid orbitals are formed by mixing atomic orbitals of comparable energies.
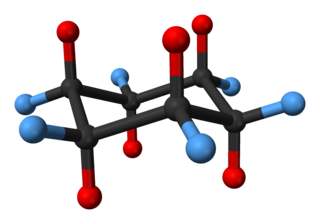
Cyclohexane conformations are any of several three-dimensional shapes adopted by molecules of cyclohexane. Because many compounds feature structurally similar six-membered rings, the structure and dynamics of cyclohexane are important prototypes of a wide range of compounds.

A potential energy surface (PES) describes the energy of a system, especially a collection of atoms, in terms of certain parameters, normally the positions of the atoms. The surface might define the energy as a function of one or more coordinates; if there is only one coordinate, the surface is called a potential energy curve or energy profile. An example is the Morse/Long-range potential.

PQS is a general purpose quantum chemistry program. Its roots go back to the first ab initio gradient program developed in Professor Peter Pulay's group but now it is developed and distributed commercially by Parallel Quantum Solutions. There is a reduction in cost for academic users and a site license. Its strong points are geometry optimization, NMR chemical shift calculations, and large MP2 calculations, and high parallel efficiency on computing clusters. It includes many other capabilities including Density functional theory, the semiempirical methods, MINDO/3, MNDO, AM1 and PM3, Molecular mechanics using the SYBYL 5.0 Force Field, the quantum mechanics/molecular mechanics mixed method using the ONIOM method, natural bond orbital (NBO) analysis and COSMO solvation models. Recently, a highly efficient parallel CCSD(T) code for closed shell systems has been developed. This code includes many other post Hartree–Fock methods: MP2, MP3, MP4, CISD, CEPA, QCISD and so on.
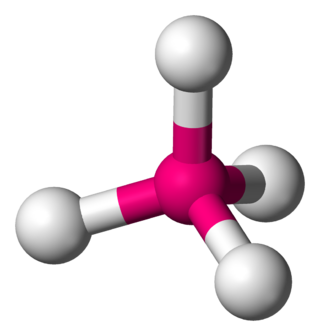
In a tetrahedral molecular geometry, a central atom is located at the center with four substituents that are located at the corners of a tetrahedron. The bond angles are cos−1(−1⁄3) = 109.4712206...° ≈ 109.5° when all four substituents are the same, as in methane as well as its heavier analogues. Methane and other perfectly symmetrical tetrahedral molecules belong to point group Td, but most tetrahedral molecules have lower symmetry. Tetrahedral molecules can be chiral.
Internal Coordinate Mechanics (ICM) is a software program and algorithm to predict low-energy conformations of molecules by sampling the space of internal coordinates defining molecular geometry. In ICM each molecule is constructed as a tree from an entry atom where each next atom is built iteratively from the preceding three atoms via three internal variables. The rings kept rigid or imposed via additional restraints. ICM is used for modelling peptides and interactions with substrates and coenzymes.
A molecular model is a physical model of an atomistic system that represents molecules and their processes. They play an important role in understanding chemistry and generating and testing hypotheses. The creation of mathematical models of molecular properties and behavior is referred to as molecular modeling, and their graphical depiction is referred to as molecular graphics.
The GF method, sometimes referred to as FG method, is a classical mechanical method introduced by Edgar Bright Wilson to obtain certain internal coordinates for a vibrating semi-rigid molecule, the so-called normal coordinatesQk. Normal coordinates decouple the classical vibrational motions of the molecule and thus give an easy route to obtaining vibrational amplitudes of the atoms as a function of time. In Wilson's GF method it is assumed that the molecular kinetic energy consists only of harmonic vibrations of the atoms, i.e., overall rotational and translational energy is ignored. Normal coordinates appear also in a quantum mechanical description of the vibrational motions of the molecule and the Coriolis coupling between rotations and vibrations.
A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies range from less than 1013 Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 µm.
In computational chemistry, a constraint algorithm is a method for satisfying the Newtonian motion of a rigid body which consists of mass points. A restraint algorithm is used to ensure that the distance between mass points is maintained. The general steps involved are: (i) choose novel unconstrained coordinates, (ii) introduce explicit constraint forces, (iii) minimize constraint forces implicitly by the technique of Lagrange multipliers or projection methods.

In chemistry, molecular symmetry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain many of a molecule's chemical properties, such as whether or not it has a dipole moment, as well as its allowed spectroscopic transitions. To do this it is necessary to use group theory. This involves classifying the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Symmetry is useful in the study of molecular orbitals, with applications to the Hückel method, to ligand field theory, and to the Woodward-Hoffmann rules. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry discuss symmetry. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materials.
In the field of computational chemistry, energy minimization is the process of finding an arrangement in space of a collection of atoms where, according to some computational model of chemical bonding, the net inter-atomic force on each atom is acceptably close to zero and the position on the potential energy surface (PES) is a stationary point. The collection of atoms might be a single molecule, an ion, a condensed phase, a transition state or even a collection of any of these. The computational model of chemical bonding might, for example, be quantum mechanics.
To determine the vibrational spectroscopy of linear molecules, the rotation and vibration of linear molecules are taken into account to predict which vibrational (normal) modes are active in the infrared spectrum and the Raman spectrum.
References
- 1 2 3 Parsons, Jerod; Holmes, J. Bradley; Rojas, J. Maurice; Tsai, Jerry; Strauss, Charlie E. M. (2005). "Practical conversion from torsion space to Cartesian space for in silico protein synthesis". Journal of Computational Chemistry. 26 (10): 1063–1068. CiteSeerX 10.1.1.83.8235 . doi:10.1002/jcc.20237. PMID 15898109. S2CID 2279574.
- ↑ Gordon, M. S.; Pople, J. A. (1968). "Approximate Self-Consistent Molecular-Orbital Theory. VI. INDO Calculated Equilibrium Geometries". The Journal of Chemical Physics. 49 (10): 4643–4650. Bibcode:1968JChPh..49.4643G. doi:10.1063/1.1669925.