Related Research Articles
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as discontinuities. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is not continuous. Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity.

In mathematical analysis, the intermediate value theorem states that if is a continuous function whose domain contains the interval [a, b], then it takes on any given value between and at some point within the interval.

In mathematics, a metric space is a set together with a notion of distance between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry.

In mathematics, a real function of real numbers is said to be uniformly continuous if there is a positive real number such that function values over any function domain interval of the size are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number , then there is a positive real number such that for any and in any interval of length within the domain of .

In mathematics, an open set is a generalization of an open interval in the real line.
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX. The Stone–Čech compactification βX of a topological space X is the largest, most general compact Hausdorff space "generated" by X, in the sense that any continuous map from X to a compact Hausdorff space factors through βX. If X is a Tychonoff space then the map from X to its image in βX is a homeomorphism, so X can be thought of as a (dense) subspace of βX; every other compact Hausdorff space that densely contains X is a quotient of βX. For general topological spaces X, the map from X to βX need not be injective.
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points form a discontinuous sequence, meaning they are isolated from each other in a certain sense. The discrete topology is the finest topology that can be given on a set. Every subset is open in the discrete topology so that in particular, every singleton subset is an open set in the discrete topology.
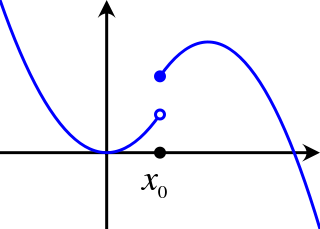
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than Briefly, a function on a domain is lower semi-continuous if its epigraph is closed in , and upper semi-continuous if is lower semi-continuous.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology.
In mathematics, an order topology is a specific topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets.
In mathematical analysis, a family of functions is equicontinuous if all the functions are continuous and they have equal variation over a given neighbourhood, in a precise sense described herein. In particular, the concept applies to countable families, and thus sequences of functions.

In mathematics, the oscillation of a function or a sequence is a number that quantifies how much that sequence or function varies between its extreme values as it approaches infinity or a point. As is the case with limits, there are several definitions that put the intuitive concept into a form suitable for a mathematical treatment: oscillation of a sequence of real numbers, oscillation of a real-valued function at a point, and oscillation of a function on an interval.
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
In geometric topology, Busemann functions are used to study the large-scale geometry of geodesics in Hadamard spaces and in particular Hadamard manifolds. They are named after Herbert Busemann, who introduced them; he gave an extensive treatment of the topic in his 1955 book "The geometry of geodesics".
In the mathematical fields of geometry and topology, a coarse structure on a set X is a collection of subsets of the cartesian product X × X with certain properties which allow the large-scale structure of metric spaces and topological spaces to be defined.
In the mathematical subject of geometric group theory, the Culler–Vogtmann Outer space or just Outer space of a free group Fn is a topological space consisting of the so-called "marked metric graph structures" of volume 1 on Fn. The Outer space, denoted Xn or CVn, comes equipped with a natural action of the group of outer automorphisms Out(Fn) of Fn. The Outer space was introduced in a 1986 paper of Marc Culler and Karen Vogtmann, and it serves as a free group analog of the Teichmüller space of a hyperbolic surface. Outer space is used to study homology and cohomology groups of Out(Fn) and to obtain information about algebraic, geometric and dynamical properties of Out(Fn), of its subgroups and individual outer automorphisms of Fn. The space Xn can also be thought of as the set of Fn-equivariant isometry types of minimal free discrete isometric actions of Fn on R-treesT such that the quotient metric graph T/Fn has volume 1.

In mathematics, a quasi-isometry is a function between two metric spaces that respects large-scale geometry of these spaces and ignores their small-scale details. Two metric spaces are quasi-isometric if there exists a quasi-isometry between them. The property of being quasi-isometric behaves like an equivalence relation on the class of metric spaces.

In mathematics, near sets are either spatially close or descriptively close. Spatially close sets have nonempty intersection. In other words, spatially close sets are not disjoint sets, since they always have at least one element in common. Descriptively close sets contain elements that have matching descriptions. Such sets can be either disjoint or non-disjoint sets. Spatially near sets are also descriptively near sets.
In mathematics, a càdlàg, RCLL, or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere. Càdlàg functions are important in the study of stochastic processes that admit jumps, unlike Brownian motion, which has continuous sample paths. The collection of càdlàg functions on a given domain is known as Skorokhod space.
In mathematics, the Earle–Hamilton fixed point theorem is a result in geometric function theory giving sufficient conditions for a holomorphic mapping of an open domain in a complex Banach space into itself to have a fixed point. The result was proved in 1968 by Clifford Earle and Richard S. Hamilton by showing that, with respect to the Carathéodory metric on the domain, the holomorphic mapping becomes a contraction mapping to which the Banach fixed-point theorem can be applied.
References
- Lowen, Robert (1997). Approach spaces: the missing link in the topology-uniformity-metric triad. Oxford Mathematical Monographs. Oxford: Clarendon Press. ISBN 0-19-850030-0. Zbl 0891.54001.
- Lowen, Robert (2015). Index Analysis: Approach Theory at Work. Springer.