Hexecontahedron

Last updated
Pentakisdodecahedron.jpg
Pentakis dodecahedron 		Deltoidalhexecontahedron.jpg
Deltoidal hexecontahedron
Pentagonalhexecontahedroncw.jpg
Pentagonal hexecontahedron 		Triakisicosahedron.jpg
Triakis icosahedron
Rhombic hexecontahedron.png
Rhombic hexecontahedron 		DU32 small hexagonal hexecontahedron.png
Small hexagonal hexecontahedron

In geometry, a hexecontahedron (or hexacontahedron [1] ) is a polyhedron with 60 faces. There are many symmetric forms, and the ones with highest symmetry have icosahedral symmetry:

Geometry branch of mathematics that measures the shape, size and position of objects

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

Polyhedron solid in three dimensions with flat faces

In geometry, a polyhedron is a solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. The word polyhedron comes from the Classical Greek πολύεδρον, as poly- + -hedron.

Icosahedral symmetry

A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation. A regular dodecahedron has the same set of symmetries, since it is the dual of the icosahedron.

Four Catalan solids, convex:

Pentakis dodecahedron polyhedron

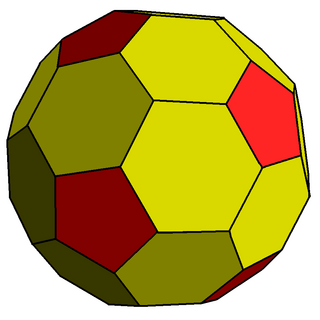
In geometry, a pentakis dodecahedron or kisdodecahedron is a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron. This interpretation is expressed in its name. There are in fact several topologically equivalent but geometrically distinct kinds of pentakis dodecahedron, depending on the height of the pentagonal pyramids. These include:

Deltoidal hexecontahedron polyhedron

In geometry, a deltoidal hexecontahedron is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices.

Pentagonal hexecontahedron polyhedron

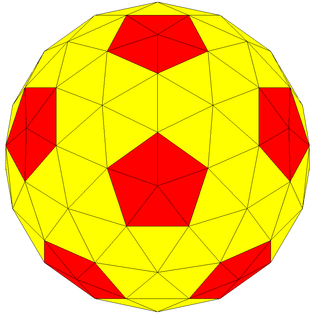
In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images of each other. It has 92 vertices that span 60 pentagonal faces. It is the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices.

Concave

27 uniform star-polyhedral duals: (self-intersecting)

Small dodecicosacron polyhedron with 60 faces

In geometry, the small dodecicosacron is the dual of the small dodecicosahedron (U50). It is visually identical to the Small ditrigonal dodecacronic hexecontahedron. It has 60 intersecting bow-tie-shaped faces.

Great dodecicosacron polyhedron with 60 faces

In geometry, the great dodecicosacron is the dual of the great dodecicosahedron (U63). It has 60 intersecting bow-tie-shaped faces.

Small rhombidodecacron

In geometry, the small rhombidodecacron is a nonconvex isohedral polyhedron. It is the dual of the small rhombidodecahedron. It is visually identical to the Small dodecacronic hexecontahedron. It has 60 intersecting antiparallelogram faces.

Related Research Articles

In geometry, a dodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

Triakis icosahedron polyhedron

In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.

Medial may refer to:

Small stellated dodecahedron Kepler-Poinsot polyhedron

In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5/2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.

Great stellated dodecahedron Kepler–Poinsot polyhedron

In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5/2,3}. It is one of four nonconvex regular polyhedra.

Small ditrigonal icosidodecahedron polyhedron with 32 faces

In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30. It has extended Schläfli symbol a{5,3}, as an altered dodecahedron, and Coxeter diagram or .

Ditrigonal dodecadodecahedron polyhedron with 24 faces

In geometry, the ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41. It has extended Schläfli symbol b{5,5/2}, as a blended great dodecahedron, and Coxeter diagram . It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 5/3 5, and Coxeter diagram .

Chamfered dodecahedron

The chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (geometry) (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.

In geometry, a simplicial polytope is a polytope whose facets are all simplices.

Small triambic icosahedron polyhedron with 20 faces

In geometry, the small triambic icosahedron is the dual to the uniform small ditrigonal icosidodecahedron. It is composed of 20 intersecting isogonal hexagon (triambus) faces. It has 60 edges and 32 vertices, and Euler characteristic of −8. Its external surface also represents the B stellation of the icosahedron.

Great triambic icosahedron polyhedron with 20 faces

In geometry, the great triambic icosahedron and medial triambic icosahedron are visually identical dual uniform polyhedra. The exterior surface also represents the De2f2 stellation of the icosahedron. The only way to differentiate these two polyhedra is to mark which intersections between edges are true vertices and which are not. In the above images, true vertices are marked by gold spheres, which can be seen in the concave Y-shaped areas.

Pentakis icosidodecahedron convex polyhedron with 80 triangular faces

The pentakis icosidodecahedron or subdivided icosahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It is a dual of the truncated rhombic triacontahedron.

Small hexagonal hexecontahedron polyhedron with 60 faces

In geometry, the small hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small snub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces.

In geometry, there are seven uniform and uniform dual polyhedra named as ditrigonal.

Order-5 truncated pentagonal hexecontahedron

The order-5 truncated pentagonal hexecontahedron is a convex polyhedron with 72 faces: 60 hexagons and 12 pentagons triangular, with 210 edges, and 140 vertices. Its dual is the pentakis snub dodecahedron.

Hexapentakis truncated icosahedron

The hexapentakis truncated icosahedron is a convex polyhedron constructed as an augmented truncated icosahedron. It is geodesic polyhedron {3,5+}3,0, with pentavalent vertices separated by an edge-direct distance of 3 steps.

References

  1. ↑ http://www.georgehart.com/virtual-polyhedra/greek-prefixes.html
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.