In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.
In geometry, an octahedron is a polyhedron with eight faces. An octahedron can be considered as a square bipyramid. When the edges of a square bipyramid are all equal in length, it produces a regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. It is also an example of a deltahedron. An octahedron is the three-dimensional case of the more general concept of a cross polytope.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:
A hexahedron or sexahedron is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex.

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron.
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.

In geometry, a deltoidal hexecontahedron is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.

In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape also has alternative names called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron; these names mean the 12-sided polyhedron.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular, quasi-regular, or semi-regular. The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
A noble polyhedron is one which is isohedral and isogonal. They were first studied in any depth by Edmund Hess and Max Brückner in the late 19th century, and later by Branko Grünbaum.

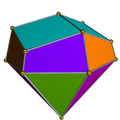
A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
14 (fourteen) is the natural number following 13 and preceding 15.
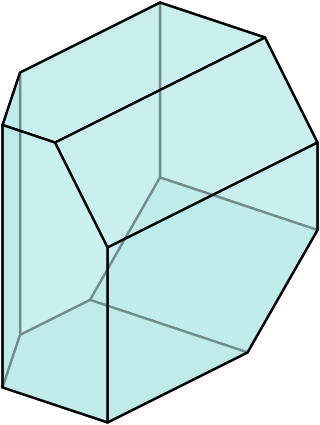
In geometry, an enneahedron is a polyhedron with nine faces. There are 2606 types of convex enneahedron, each having a different pattern of vertex, edge, and face connections. None of them are regular.

In geometry, an octadecahedron is a polyhedron with 18 faces. No octadecahedron is regular; hence, the name does not commonly refer to one specific polyhedron.

A tridecahedron, or triskaidecahedron, is a polyhedron with thirteen faces. There are numerous topologically distinct forms of a tridecahedron, for example the dodecagonal pyramid and hendecagonal prism. However, a tridecahedron cannot be a regular polyhedron, because there is no regular polygon that can form a regular tridecahedron, and there are only five known regular convex polyhedra.

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.