Pentahedron

For the Sylvester pentahedron of a cubic surface, see quaternary cubic.

In geometry, a pentahedron (pl.: pentahedra) is a polyhedron with five faces or sides. There are no face-transitive polyhedra with five sides, and there are two distinct topological types. Notable polyhedra with regular polygon faces are:

• 
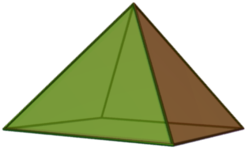
  Square pyramid with four triangles and one square. ^[1] Pyramids with any quadrilateral base have the same number of faces.
• 
  Triangular prism with three rectangles and two triangular bases. ^[1] In the case of a right triangular prism, it is a special case of wedge with connecting parallel edges between triangles; the wedge generally has two triangles and three quadrilateral faces. ^[2] Topologically, the triangular frustum is the same polyhedron, but the two triangles are different sizes, and the sides are slanted trapezoids.

The pentahedra can be used as space-filling. ^{[3] [4]}

Concave

Above: a concave pentahedron viewed from its apex. Below: the same object viewed from its concave face.

An irregular pentahedron can be a non-convex solid: Consider a non-convex (planar) quadrilateral (such as a dart) as the base of the solid, and any point not in the base plane as the apex.

Hosohedron

There is a third topological polyhedral figure with 5 faces, degenerate as a polyhedron: it exists as a spherical tiling of digon faces, called a pentagonal hosohedron with Schläfli symbol {2,5}. It has 2 (antipodal point) vertices, 5 edges, and 5 digonal faces.

References

1. Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR   0290245.
2. Haul, Wm. S. (1893). Mensuration. Ginn & Company. p. 45.
3. Goldberg, Michael (1972). "The space-filling pentahedra". Journal of Combinatorial Theory, Series A. 13 (3): 437–443.
4. Goldberg, Michael (1974). "The space-filling pentahedra. II". Journal of Combinatorial Theory, Series A. 17 (3): 375–378.

External links

• Weisstein, Eric W. "Pentahedron". MathWorld .