In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.
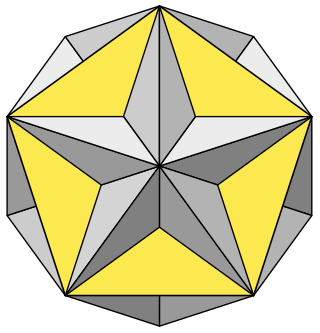
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A hexahedron or sexahedron is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex.
In geometry, a pentahedron is a polyhedron with five faces or sides. There are no face-transitive polyhedra with five sides and there are two distinct topological types.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .

In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.

A heptahedron is a polyhedron having seven sides, or faces.

In geometry, a toroidal polyhedron is a polyhedron which is also a toroid, having a topological genus of 1 or greater. Notable examples include the Császár and Szilassi polyhedra.

In geometry, the excavated dodecahedron is a star polyhedron that looks like a dodecahedron with concave pentagonal pyramids in place of its faces. Its exterior surface represents the Ef1g1 stellation of the icosahedron. It appears in Magnus Wenninger's book Polyhedron Models as model 28, the third stellation of icosahedron.
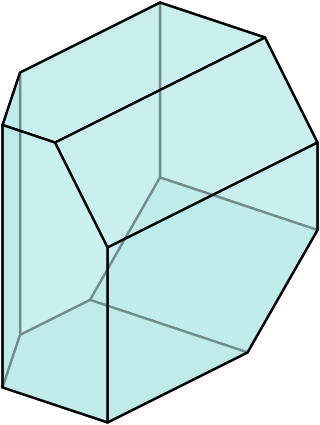
In geometry, an enneahedron is a polyhedron with nine faces. There are 2606 types of convex enneahedron, each having a different pattern of vertex, edge, and face connections. None of them are regular.

In geometry, an octadecahedron is a polyhedron with 18 faces. No octadecahedron is regular; hence, the name does not commonly refer to one specific polyhedron.

A hendecahedron is a polyhedron with 11 faces. There are numerous topologically distinct forms of a hendecahedron, for example the decagonal pyramid, and enneagonal prism.

A tridecahedron, or triskaidecahedron, is a polyhedron with thirteen faces. There are numerous topologically distinct forms of a tridecahedron, for example the dodecagonal pyramid and hendecagonal prism. However, a tridecahedron cannot be a regular polyhedron, because there is no regular polygon that can form a regular tridecahedron, and there are only five known regular polyhedra.

A pentadecahedron is a polyhedron with 15 faces. No pentadecahedron is regular; hence, the name is ambiguous. There are numerous topologically distinct forms of a pentadecahedron, for example the tetradecagonal pyramid, and tridecagonal prism. In the pentadecahedron, none of the shapes are regular polyhedra, in other words, the regular pentadecahedron does not exist, and the pentadecahedron cannot fill the space, or, a space-filling pentadecahedron does not exist.
A hexadecahedron is a polyhedron with 16 faces. No hexadecahedron is regular; hence, the name is ambiguous. There are numerous topologically distinct forms of a hexadecahedron, for example the pentadecagonal pyramid, tetradecagonal prism and heptagonal antiprism.
A heptadecahedron is a polyhedron with 17 faces. No heptadecahedron is regular; hence, the name is ambiguous. There are numerous topologically distinct forms of a heptadecahedron, for example the hexadecagonal pyramid and pentadecagonal prism.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.


















