| Common tridecahedra | |
|---|---|
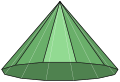
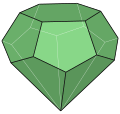
 Space-filling tridecahedron |  Elongated hexagonal pyramid |
 Hendecagonal prism |  Gyroelongated square pyramid |
A tridecahedron, or triskaidecahedron, is a polyhedron with thirteen faces. There are numerous topologically distinct forms of a tridecahedron, for example the dodecagonal pyramid and hendecagonal prism. However, a tridecahedron cannot be a regular polyhedron, because there is no regular polygon that can form a regular tridecahedron, and there are only five known regular convex polyhedra. [notes 1] [1]