In cryptography, a block cipher is a deterministic algorithm operating on fixed-length groups of bits, called blocks. It uses an unvarying transformation, that is, it uses a symmetric key. They are specified elementary components in the design of many cryptographic protocols and are widely used to implement the encryption of large amounts of data, including data exchange protocols.

Cryptanalysis is the study of analyzing information systems in order to study the hidden aspects of the systems. Cryptanalysis is used to breach cryptographic security systems and gain access to the contents of encrypted messages, even if the cryptographic key is unknown.
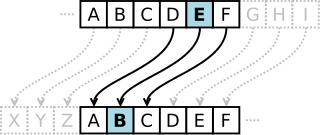
In cryptography, a Caesar cipher, also known as Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on. The method is named after Julius Caesar, who used it in his private correspondence.
In cryptography, linear cryptanalysis is a general form of cryptanalysis based on finding affine approximations to the action of a cipher. Attacks have been developed for block ciphers and stream ciphers. Linear cryptanalysis is one of the two most widely used attacks on block ciphers; the other being differential cryptanalysis.

The Vigenère cipher is a method of encrypting alphabetic text by using a series of interwoven Caesar ciphers, based on the letters of a keyword. It employs a form of polyalphabetic substitution.
Malleability is a property of some cryptographic algorithms. An encryption algorithm is "malleable" if it is possible to transform a ciphertext into another ciphertext which decrypts to a related plaintext. That is, given an encryption of a plaintext , it is possible to generate another ciphertext which decrypts to , for a known function , without necessarily knowing or learning .
In cryptography, an initialization vector (IV) or starting variable (SV) is a fixed-size input to a cryptographic primitive that is typically required to be random or pseudorandom. Randomization is crucial for encryption schemes to achieve semantic security, a property whereby repeated usage of the scheme under the same key does not allow an attacker to infer relationships between segments of the encrypted message. For block ciphers, the use of an IV is described by the modes of operation. Randomization is also required for other primitives, such as universal hash functions and message authentication codes based thereon.

In cryptography, the tabula recta is a square table of alphabets, each row of which is made by shifting the previous one to the left. The term was invented by the German author and monk Johannes Trithemius in 1508, and used in his Trithemius cipher.
In cryptography, a block cipher mode of operation is an algorithm that uses a block cipher to provide information security such as confidentiality or authenticity. A block cipher by itself is only suitable for the secure cryptographic transformation of one fixed-length group of bits called a block. A mode of operation describes how to repeatedly apply a cipher's single-block operation to securely transform amounts of data larger than a block.

In cryptography, ciphertext or cyphertext is the result of encryption performed on plaintext using an algorithm, called a cipher. Ciphertext is also known as encrypted or encoded information because it contains a form of the original plaintext that is unreadable by a human or computer without the proper cipher to decrypt it. Decryption, the inverse of encryption, is the process of turning ciphertext into readable plaintext. Ciphertext is not to be confused with codetext because the latter is a result of a code, not a cipher.
In cryptography, a Feistel cipher is a symmetric structure used in the construction of block ciphers, named after the German-born physicist and cryptographer Horst Feistel who did pioneering research while working for IBM (USA); it is also commonly known as a Feistel network. A large proportion of block ciphers use the scheme, including the US Data Encryption Standard, the Soviet/Russian GOST and the more recent Blowfish and Twofish ciphers. In a Feistel cipher, encryption and decryption are very similar operations, and both consist of iteratively running a function called a "round function" a fixed number of times.
The meet-in-the-middle attack (MITM), a known plaintext attack, is a generic space–time tradeoff cryptographic attack against encryption schemes that rely on performing multiple encryption operations in sequence. The MITM attack is the primary reason why Double DES is not used and why a Triple DES key (168-bit) can be bruteforced by an attacker with 256 space and 2112 operations.

In cryptography, DES-X is a variant on the DES symmetric-key block cipher intended to increase the complexity of a brute-force attack using a technique called key whitening.
In cryptography, Optimal Asymmetric Encryption Padding (OAEP) is a padding scheme often used together with RSA encryption. OAEP was introduced by Bellare and Rogaway, and subsequently standardized in PKCS#1 v2 and RFC 2437.

In cryptography, the boomerang attack is a method for the cryptanalysis of block ciphers based on differential cryptanalysis. The attack was published in 1999 by David Wagner, who used it to break the COCONUT98 cipher.
In cryptography, an interpolation attack is a type of cryptanalytic attack against block ciphers.

In cryptography, a one-way compression function is a function that transforms two fixed-length inputs into a fixed-length output. The transformation is "one-way", meaning that it is difficult given a particular output to compute inputs which compress to that output. One-way compression functions are not related to conventional data compression algorithms, which instead can be inverted exactly or approximately to the original data.
In cryptography, M8 is a block cipher designed by Hitachi in 1999. The algorithm negotiates introduced in 1997 M6, with the modified key length, which is enlarged to 64 bits or more. This cipher operates with Feistel network and designed to reach high performance on small implementation or 32 bits devices. For instance, by using round numbers = 10 it present encryption speed at 32 Mbps for dedicated hardware of 6K gates and 25 MHz clock or 208 Mbps for program, that uses C-language and Pentium-I 266 MHz. Due to the openness of description, it should not be used in open or multivendor software.
The 3-subset meet-in-the-middleattack is a variant of the generic meet-in-the-middle attack, which is used in cryptology for hash and block cipher cryptanalysis. The 3-subset variant opens up the possibility to apply MITM attacks on ciphers, where it is not trivial to divide the keybits into two independent key-spaces, as required by the MITM attack.
A time/memory/data tradeoff attack is a type of cryptographic attack where an attacker tries to achieve a situation similar to the space–time tradeoff but with one more parameter data: amount of data available to the attacker at real time. An attacker balances or reduces one or two of those parameters in favor of the other one or two. This type of attack is very hard and most of the ciphers and encryption schemes were not designed to resist such type of attack. This attack is a special type of the general cryptanalytic time/memory tradeoff attack.





















