KASUMI

KASUMI

General
Designers	Mitsubishi Electric
Derived from	MISTY1
Cipher detail
Key sizes	128 bits
Block sizes	64 bits
Structure	Feistel network
Rounds	8

KASUMI is a block cipher used in UMTS, GSM, and GPRS mobile communications systems. In UMTS, KASUMI is used in the confidentiality (f8) and integrity algorithms (f9) with names UEA1 and UIA1, respectively. ^[1] In GSM, KASUMI is used in the A5/3 key stream generator and in GPRS in the GEA3 key stream generator.

KASUMI was designed for 3GPP to be used in UMTS security system by the Security Algorithms Group of Experts (SAGE), a part of the European standards body ETSI. ^[2] Because of schedule pressures in 3GPP standardization, instead of developing a new cipher, SAGE agreed with 3GPP technical specification group (TSG) for system aspects of 3G security (SA3) to base the development on an existing algorithm that had already undergone some evaluation. ^[2] They chose the cipher algorithm MISTY1 developed ^[3] and patented ^[4] by Mitsubishi Electric Corporation. The original algorithm was slightly modified for easier hardware implementation and to meet other requirements set for 3G mobile communications security.

KASUMI is named after the original algorithm MISTY1 — 霞み (hiragana かすみ, romaji kasumi ) is the Japanese word for "mist".

In January 2010, Orr Dunkelman, Nathan Keller and Adi Shamir released a paper showing that they could break Kasumi with a related-key attack and very modest computational resources; this attack is ineffective against MISTY1. ^[5]

Description

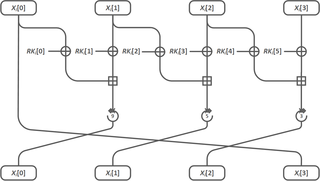
KASUMI algorithm is specified in a 3GPP technical specification. ^[6] KASUMI is a block cipher with 128-bit key and 64-bit input and output. The core of KASUMI is an eight-round Feistel network. The round functions in the main Feistel network are irreversible Feistel-like network transformations. In each round the round function uses a round key which consists of eight 16-bit sub keys derived from the original 128-bit key using a fixed key schedule.

Key schedule

The 128-bit key K is divided into eight 16-bit sub keys K_i:

${\displaystyle K=K_{1}\|K_{2}\|K_{3}\|K_{4}\|K_{5}\|K_{6}\|K_{7}\|K_{8}\,}$

Additionally a modified key K', similarly divided into 16-bit sub keys K'_i, is used. The modified key is derived from the original key by XORing with 0x123456789ABCDEFFEDCBA9876543210 (chosen as a "nothing up my sleeve" number).

Round keys are either derived from the sub keys by bitwise rotation to left by a given amount and from the modified sub keys (unchanged).

The round keys are as follows:

${\displaystyle {\begin{array}{lcl}KL_{i,1}&=&{\rm {ROL}}(K_{i},1)\\KL_{i,2}&=&K'_{i+2}\\KO_{i,1}&=&{\rm {ROL}}(K_{i+1},5)\\KO_{i,2}&=&{\rm {ROL}}(K_{i+5},8)\\KO_{i,3}&=&{\rm {ROL}}(K_{i+6},13)\\KI_{i,1}&=&K'_{i+4}\\KI_{i,2}&=&K'_{i+3}\\KI_{i,3}&=&K'_{i+7}\end{array}}}$

Sub key index additions are cyclic so that if i+j is greater than 8 one has to subtract 8 from the result to get the actual sub key index.

The algorithm

KASUMI algorithm processes the 64-bit word in two 32-bit halves, left (${\displaystyle L_{i}}$) and right (${\displaystyle R_{i}}$). The input word is concatenation of the left and right halves of the first round:

${\displaystyle {\rm {input}}=R_{0}\|L_{0}\,}$.

In each round the right half is XOR'ed with the output of the round function after which the halves are swapped:

${\displaystyle {\begin{array}{rcl}L_{i}&=&F_{i}(KL_{i},KO_{i},KI_{i},L_{i-1})\oplus R_{i-1}\\R_{i}&=&L_{i-1}\end{array}}}$

where KL_i, KO_i, KI_i are round keys for the i^th round.

The round functions for even and odd rounds are slightly different. In each case the round function is a composition of two functions FL_i and FO_i. For an odd round

${\displaystyle F_{i}(K_{i},L_{i-1})=FO(KO_{i},KI_{i},FL(KL_{i},L_{i-1}))\,}$

and for an even round

${\displaystyle F_{i}(K_{i},L_{i-1})=FL(KL_{i},FO(KO_{i},KI_{i},L_{i-1}))\,}$.

The output is the concatenation of the outputs of the last round.

${\displaystyle {\rm {output}}=R_{8}\|L_{8}\,}$.

Both FL and FO functions divide the 32-bit input data to two 16-bit halves. The FL function is an irreversible bit manipulation while the FO function is an irreversible three round Feistel-like network.

Function FL

The 32-bit input x of ${\displaystyle FL(KL_{i},x)}$ is divided to two 16-bit halves ${\displaystyle x=l\|r}$. First the left half of the input ${\displaystyle l}$ is ANDed bitwise with round key ${\displaystyle KL_{i,1}}$ and rotated left by one bit. The result of that is XOR'ed to the right half of the input ${\displaystyle r}$ to get the right half of the output ${\displaystyle r'}$.

${\displaystyle r'={\rm {ROL}}(l\wedge KL_{i,1},1)\oplus r}$

Then the right half of the output ${\displaystyle r'}$ is ORed bitwise with the round key ${\displaystyle KL_{i,2}}$ and rotated left by one bit. The result of that is XOR'ed to the left half of the input ${\displaystyle l}$ to get the left half of the output ${\displaystyle l'}$.

${\displaystyle l'={\rm {ROL}}(r'\vee KL_{i,2},1)\oplus l}$

Output of the function is concatenation of the left and right halves ${\displaystyle x'=l'\|r'}$.

Function FO

The 32-bit input x of ${\displaystyle FO(KO_{i},KI_{i},x)}$ is divided into two 16-bit halves ${\displaystyle x=l_{0}\|r_{0}}$, and passed through three rounds of a Feistel network.

In each of the three rounds (indexed by j that takes values 1, 2, and 3) the left half is modified to get the new right half and the right half is made the left half of the next round.

${\displaystyle {\begin{array}{lcl}r_{j}&=&FI(KI_{i,j},l_{j-1}\oplus KO_{i,j})\oplus r_{j-1}\\l_{j}&=&r_{j-1}\end{array}}}$

The output of the function is ${\displaystyle x'=l_{3}\|r_{3}}$.

Function FI

The function FI is an irregular Feistel-like network.

The 16-bit input ${\displaystyle x}$ of the function ${\displaystyle FI(Ki,x)}$ is divided to two halves ${\displaystyle x=l_{0}\|r_{0}}$ of which ${\displaystyle l_{0}}$ is 9 bits wide and ${\displaystyle r_{0}}$ is 7 bits wide.

Bits in the left half ${\displaystyle l_{0}}$ are first shuffled by 9-bit substitution box (S-box) S9 and the result is XOR'ed with the zero-extended right half ${\displaystyle r_{0}}$ to get the new 9-bit right half ${\displaystyle r_{1}}$.

${\displaystyle r_{1}=S9(l_{0})\oplus (00\|r_{0})\,}$

Bits of the right half ${\displaystyle r_{0}}$ are shuffled by 7-bit S-box S7 and the result is XOR'ed with the seven least significant bits (LS7) of the new right half ${\displaystyle r_{1}}$ to get the new 7-bit left half ${\displaystyle l_{1}}$.

${\displaystyle l_{1}=S7(r_{0})\oplus LS7(r_{1})\,}$

The intermediate word ${\displaystyle x_{1}=l_{1}\|r_{1}}$ is XORed with the round key KI to get ${\displaystyle x_{2}=l_{2}\|r_{2}}$ of which ${\displaystyle l_{2}}$ is 7 bits wide and ${\displaystyle r_{2}}$ is 9 bits wide.

${\displaystyle x_{2}=KI\oplus x_{1}}$

Bits in the right half ${\displaystyle r_{2}}$ are then shuffled by 9-bit S-box S9 and the result is XOR'ed with the zero-extended left half ${\displaystyle l_{2}}$ to get the new 9-bit right half of the output ${\displaystyle r_{3}}$.

${\displaystyle r_{3}=S9(r_{2})\oplus (00\|l_{2})\,}$

Finally the bits of the left half ${\displaystyle l_{2}}$ are shuffled by 7-bit S-box S7 and the result is XOR'ed with the seven least significant bits (LS7) of the right half of the output ${\displaystyle r_{3}}$ to get the 7-bit left half ${\displaystyle l_{3}}$ of the output.

${\displaystyle l_{3}=S7(l_{2})\oplus LS7(r_{3})\,}$

The output is the concatenation of the final left and right halves ${\displaystyle x'=l_{3}\|r_{3}}$.

Substitution boxes

The substitution boxes (S-boxes) S7 and S9 are defined by both bit-wise AND-XOR expressions and look-up tables in the specification. The bit-wise expressions are intended to hardware implementation but nowadays it is customary to use the look-up tables even in the HW design.

S7 is defined by the following array:

intS7[128]={54,50,62,56,22,34,94,96,38,6,63,93,2,18,123,33,55,113,39,114,21,67,65,12,47,73,46,27,25,111,124,81,53,9,121,79,52,60,58,48,101,127,40,120,104,70,71,43,20,122,72,61,23,109,13,100,77,1,16,7,82,10,105,98,117,116,76,11,89,106,0,125,118,99,86,69,30,57,126,87,112,51,17,5,95,14,90,84,91,8,35,103,32,97,28,66,102,31,26,45,75,4,85,92,37,74,80,49,68,29,115,44,64,107,108,24,110,83,36,78,42,19,15,41,88,119,59,3};

S9 is defined by the following array:

intS9[512]={167,239,161,379,391,334,9,338,38,226,48,358,452,385,90,397,183,253,147,331,415,340,51,362,306,500,262,82,216,159,356,177,175,241,489,37,206,17,0,333,44,254,378,58,143,220,81,400,95,3,315,245,54,235,218,405,472,264,172,494,371,290,399,76,165,197,395,121,257,480,423,212,240,28,462,176,406,507,288,223,501,407,249,265,89,186,221,428,164,74,440,196,458,421,350,163,232,158,134,354,13,250,491,142,191,69,193,425,152,227,366,135,344,300,276,242,437,320,113,278,11,243,87,317,36,93,496,27,487,446,482,41,68,156,457,131,326,403,339,20,39,115,442,124,475,384,508,53,112,170,479,151,126,169,73,268,279,321,168,364,363,292,46,499,393,327,324,24,456,267,157,460,488,426,309,229,439,506,208,271,349,401,434,236,16,209,359,52,56,120,199,277,465,416,252,287,246,6,83,305,420,345,153,502,65,61,244,282,173,222,418,67,386,368,261,101,476,291,195,430,49,79,166,330,280,383,373,128,382,408,155,495,367,388,274,107,459,417,62,454,132,225,203,316,234,14,301,91,503,286,424,211,347,307,140,374,35,103,125,427,19,214,453,146,498,314,444,230,256,329,198,285,50,116,78,410,10,205,510,171,231,45,139,467,29,86,505,32,72,26,342,150,313,490,431,238,411,325,149,473,40,119,174,355,185,233,389,71,448,273,372,55,110,178,322,12,469,392,369,190,1,109,375,137,181,88,75,308,260,484,98,272,370,275,412,111,336,318,4,504,492,259,304,77,337,435,21,357,303,332,483,18,47,85,25,497,474,289,100,269,296,478,270,106,31,104,433,84,414,486,394,96,99,154,511,148,413,361,409,255,162,215,302,201,266,351,343,144,441,365,108,298,251,34,182,509,138,210,335,133,311,352,328,141,396,346,123,319,450,281,429,228,443,481,92,404,485,422,248,297,23,213,130,466,22,217,283,70,294,360,419,127,312,377,7,468,194,2,117,295,463,258,224,447,247,187,80,398,284,353,105,390,299,471,470,184,57,200,348,63,204,188,33,451,97,30,310,219,94,160,129,493,64,179,263,102,189,207,114,402,438,477,387,122,192,42,381,5,145,118,180,449,293,323,136,380,43,66,60,455,341,445,202,432,8,237,15,376,436,464,59,461};

Cryptanalysis

In 2001, an impossible differential attack on six rounds of KASUMI was presented by Kühn (2001). ^[7]

In 2003 Elad Barkan, Eli Biham and Nathan Keller demonstrated man-in-the-middle attacks against the GSM protocol which avoided the A5/3 cipher and thus breaking the protocol. This approach does not attack the A5/3 cipher, however. ^[8] The full version of their paper was published later in 2006. ^[9]

In 2005, Israeli researchers Eli Biham, Orr Dunkelman and Nathan Keller published a related-key rectangle (boomerang) attack on KASUMI that can break all 8 rounds faster than exhaustive search. ^[10] The attack requires 2^54.6 chosen plaintexts, each of which has been encrypted under one of four related keys, and has a time complexity equivalent to 2^76.1 KASUMI encryptions. While this is obviously not a practical attack, it invalidates some proofs about the security of the 3GPP protocols that had relied on the presumed strength of KASUMI.

In 2010, Dunkelman, Keller and Shamir published a new attack that allows an adversary to recover a full A5/3 key by related-key attack. ^[5] The time and space complexities of the attack are low enough that the authors carried out the attack in two hours on an Intel Core 2 Duo desktop computer even using the unoptimized reference KASUMI implementation. The authors note that this attack may not be applicable to the way A5/3 is used in 3G systems; their main purpose was to discredit 3GPP's assurances that their changes to MISTY wouldn't significantly impact the security of the algorithm.

See also

• A5/1 and A5/2
• SNOW

References

1. "Draft Report of SA3 #38" (PDF). 3GPP. 2005.
2. "General Report on the Design, Speification and Evaluation of 3GPP Standard Confidentiality and Integrity Algorithms" (PDF). 3GPP. 2009.
3. Matsui, Mitsuru; Tokita, Toshio (Dec 2000). "MISTY, KASUMI and Camellia Cipher Algorithm Development" (PDF). Mitsubishi Electric Advance. Mitsubishi Electric corp. 100: 2–8. ISSN   1345-3041. Archived from the original (PDF) on 2008-07-24. Retrieved 2010-01-06.
4. US 7096369,Matsui, Mitsuru&Tokita, Toshio,"Data Transformation Apparatus and Data Transformation Method",published Sep. 19, 2002,issued Aug. 22, 2006 
5. Orr Dunkelman; Nathan Keller; Adi Shamir (2010-01-10). "A Practical-Time Attack on the A5/3 Cryptosystem Used in Third Generation GSM Telephony".
6. "3GPP TS 35.202: Specification of the 3GPP confidentiality and integrity algorithms; Document 2: Kasumi specification". 3GPP. 2009.
7. Kühn, Ulrich. Cryptanalysis of Reduced Round MISTY. EUROCRYPT 2001. CiteSeerX   10.1.1.59.7609 .
8. Elad Barkan, Eli Biham, Nathan Keller. Instant Ciphertext-Only Cryptanalysis of GSM Encrypted Communication (PDF). CRYPTO 2003. pp. 600–616.
9. Elad Barkan, Eli Biham, Nathan Keller. "Instant Ciphertext-Only Cryptanalysis of GSM Encrypted Communication by Barkan and Biham of Technion (Full Version)" (PDF).
10. Eli Biham, Orr Dunkelman, Nathan Keller. A Related-Key Rectangle Attack on the Full KASUMI. ASIACRYPT 2005. pp. 443–461. Archived from the original (ps) on 2013-10-11.

External links

• Nathan Keller's homepage