Truncated differential cryptanalysis

Last updated

In cryptography, truncated differential cryptanalysis is a generalization of differential cryptanalysis, an attack against block ciphers. Lars Knudsen developed the technique in 1994. Whereas ordinary differential cryptanalysis analyzes the full difference between two texts, the truncated variant considers differences that are only partially determined. That is, the attack makes predictions of only some of the bits instead of the full block. This technique has been applied to SAFER, IDEA, Skipjack, E2, Twofish, Camellia, CRYPTON, and even the stream cipher Salsa20.

Related Research Articles

In cryptography, Skipjack is a block cipher—an algorithm for encryption—developed by the U.S. National Security Agency (NSA). Initially classified, it was originally intended for use in the controversial Clipper chip. Subsequently, the algorithm was declassified.

In cryptography, SHARK is a block cipher identified as one of the predecessors of Rijndael.

In cryptography, SAFER is the name of a family of block ciphers designed primarily by James Massey on behalf of Cylink Corporation. The early SAFER K and SAFER SK designs share the same encryption function, but differ in the number of rounds and the key schedule. More recent versions — SAFER+ and SAFER++ — were submitted as candidates to the AES process and the NESSIE project respectively. All of the algorithms in the SAFER family are unpatented and available for unrestricted use.

In cryptography, Khufu and Khafre are two block ciphers designed by Ralph Merkle in 1989 while working at Xerox's Palo Alto Research Center. Along with Snefru, a cryptographic hash function, the ciphers were named after the Egyptian Pharaohs Khufu, Khafre and Sneferu.

In cryptography, LOKI89 and LOKI91 are symmetric-key block ciphers designed as possible replacements for the Data Encryption Standard (DES). The ciphers were developed based on a body of work analysing DES, and are very similar to DES in structure. The LOKI algorithms were named for Loki, the god of mischief in Norse mythology.

MacGuffin (cipher)

In cryptography, MacGuffin is a block cipher created in 1994 by Bruce Schneier and Matt Blaze at a Fast Software Encryption workshop. It was intended as a catalyst for analysis of a new cipher structure, known as Generalized Unbalanced Feistel Networks (GUFNs). The cryptanalysis proceeded very quickly, so quickly that the cipher was broken at the same workshop by Vincent Rijmen and Bart Preneel.

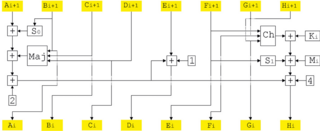
SHACAL

SHACAL-1 is a 160-bit block cipher based on SHA-1, and supports keys from 128-bit to 512-bit. SHACAL-2 is a 256-bit block cipher based upon the larger hash function SHA-256.

Boomerang attack

In cryptography, the boomerang attack is a method for the cryptanalysis of block ciphers based on differential cryptanalysis. The attack was published in 1999 by David Wagner, who used it to break the COCONUT98 cipher.

Introduced by Martin Hellman and Susan K. Langford in 1994, the differential-linear attack is a mix of both linear cryptanalysis and differential cryptanalysis.

In cryptography, higher-order differential cryptanalysis is a generalization of differential cryptanalysis, an attack used against block ciphers. While in standard differential cryptanalysis the difference between only two texts is used, higher-order differential cryptanalysis studies the propagation of a set of differences between a larger set of texts. Xuejia Lai, in 1994, laid the groundwork by showing that differentials are a special case of the more general case of higher order derivates. Lars Knudsen, in the same year, was able to show how the concept of higher order derivatives can be used to mount attacks on block ciphers. These attacks can be superior to standard differential cryptanalysis. Higher-order differential cryptanalysis has notably been used to break the KN-Cipher, a cipher which had previously been proved to be immune against standard differential cryptanalysis.

In cryptography, impossible differential cryptanalysis is a form of differential cryptanalysis for block ciphers. While ordinary differential cryptanalysis tracks differences that propagate through the cipher with greater than expected probability, impossible differential cryptanalysis exploits differences that are impossible at some intermediate state of the cipher algorithm.

In cryptography, integral cryptanalysis is a cryptanalytic attack that is particularly applicable to block ciphers based on substitution–permutation networks. It was originally designed by Lars Knudsen as a dedicated attack against Square, so it is commonly known as the Square attack. It was also extended to a few other ciphers related to Square: CRYPTON, Rijndael, and SHARK. Stefan Lucks generalized the attack to what he called a saturation attack and used it to attack Twofish, which is not at all similar to Square, having a radically different Feistel network structure. Forms of integral cryptanalysis have since been applied to a variety of ciphers, including Hierocrypt, IDEA, Camellia, Skipjack, MISTY1, MISTY2, SAFER++, KHAZAD, and FOX.

In cryptography, DFC is a symmetric block cipher which was created in 1998 by a group of researchers from École Normale Supérieure, CNRS, and France Télécom and submitted to the AES competition.

An MDS matrix is a matrix representing a function with certain diffusion properties that have useful applications in cryptography. Technically, an m×n matrix A over a finite field K is an MDS matrix if it is the transformation matrix of a linear transformation f(x)=Ax from Kn to Km such that no two different (m+n)-tuples of the form coincide in n or more components. Equivalently, the set of all (m+n)-tuples is an MDS code, i.e. a linear code that reaches the Singleton bound.

In cryptography, KN-Cipher is a block cipher created by Kaisa Nyberg and Lars Knudsen in 1995. One of the first ciphers designed to be provably secure against ordinary differential cryptanalysis, KN-Cipher was later broken using higher order differential cryptanalysis.

In cryptography, xmx is a block cipher designed in 1997 by David M'Raïhi, David Naccache, Jacques Stern, and Serge Vaudenay. According to the designers it "uses public-key-like operations as confusion and diffusion means." The cipher was designed for efficiency, and the only operations it uses are XORs and modular multiplications.

In cryptography, COCONUT98 is a block cipher designed by Serge Vaudenay in 1998. It was one of the first concrete applications of Vaudenay's decorrelation theory, designed to be provably secure against differential cryptanalysis, linear cryptanalysis, and even certain types of undiscovered cryptanalytic attacks.

In cryptography, decorrelation theory is a system developed by Serge Vaudenay in 1998 for designing block ciphers to be provably secure against differential cryptanalysis, linear cryptanalysis, and even undiscovered cryptanalytic attacks meeting certain broad criteria. Ciphers designed using these principles include COCONUT98 and the AES candidate DFC, both of which have been shown to be vulnerable to some forms of cryptanalysis not covered by the theory.

In cryptography, partitioning cryptanalysis is a form of cryptanalysis for block ciphers. Developed by Carlo Harpes in 1995, the attack is a generalization of linear cryptanalysis. Harpes originally replaced the bit sums of linear cryptanalysis with more general balanced Boolean functions. He demonstrated a toy cipher that exhibits resistance against ordinary linear cryptanalysis but is susceptible to this sort of partitioning cryptanalysis. In its full generality, partitioning cryptanalysis works by dividing the sets of possible plaintexts and ciphertexts into efficiently-computable partitions such that the distribution of ciphertexts is significantly non-uniform when the plaintexts are chosen uniformly from a given block of the partition. Partitioning cryptanalysis has been shown to be more effective than linear cryptanalysis against variants of DES and CRYPTON. A specific partitioning attack called mod n cryptanalysis uses the congruence classes modulo some integer for partitions.

In cryptography, MultiSwap is a block cipher/MAC created by Microsoft in 1999 as part of its Windows Media DRM service (WMDRM). Microsoft's internal name for the algorithm is not publicly known; it was dubbed MultiSwap in a 2001 report on WMDRM under the pseudonym "Beale Screamer".

References


This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.