In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all limiting values of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval [0,1] would be compact. Similarly, the space of rational numbers is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers is not compact either, because it excludes the two limiting values and . However, the extended real number linewould be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces.

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces.
In topology and related areas of mathematics, a product space is the Cartesian product of a family of topological spaces equipped with a natural topology called the product topology. This topology differs from another, perhaps more natural-seeming, topology called the box topology, which can also be given to a product space and which agrees with the product topology when the product is over only finitely many spaces. However, the product topology is "correct" in that it makes the product space a categorical product of its factors, whereas the box topology is too fine; in that sense the product topology is the natural topology on the Cartesian product.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology. For a list of terms specific to algebraic topology, see Glossary of algebraic topology.

In topology, the Tietze extension theorem states that any real-valued, continuous function on a closed subset of a normal topological space can be extended to the entire space, preserving boundedness if necessary.
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis. A topological vector space is a vector space that is also a topological space with the property that the vector space operations are also continuous functions. Such a topology is called a vector topology and every topological vector space has a uniform topological structure, allowing a notion of uniform convergence and completeness. Some authors also require that the space is a Hausdorff space. One of the most widely studied categories of TVSs are locally convex topological vector spaces. This article focuses on TVSs that are not necessarily locally convex. Other well-known examples of TVSs include Banach spaces, Hilbert spaces and Sobolev spaces.
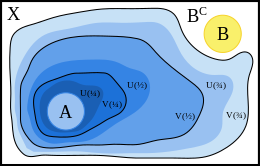
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space. These conditions are examples of separation axioms and their further strengthenings define completely normal Hausdorff spaces, or T5 spaces, and perfectly normal Hausdorff spaces, or T6 spaces.
In mathematics, a paracompact space is a topological space in which every open cover has an open refinement that is locally finite. These spaces were introduced by Dieudonné (1944). Every compact space is paracompact. Every paracompact Hausdorff space is normal, and a Hausdorff space is paracompact if and only if it admits partitions of unity subordinate to any open cover. Sometimes paracompact spaces are defined so as to always be Hausdorff.
In real analysis the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way: roughly speaking, neither overlapping nor touching. The notion of when two sets are separated or not is important both to the notion of connected spaces as well as to the separation axioms for topological spaces.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology.

In topology and related areas of mathematics, the quotient space of a topological space under a given equivalence relation is a new topological space constructed by endowing the quotient set of the original topological space with the quotient topology, that is, with the finest topology that makes continuous the canonical projection map. In other words, a subset of a quotient space is open if and only if its preimage under the canonical projection map is open in the original topological space.
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed. It is the smallest example of a topological space which is neither trivial nor discrete. It is named after Wacław Sierpiński.
In topology and related areas of mathematics, a topological property or topological invariant is a property of a topological space that is invariant under homeomorphisms. Alternatively, a topological property is a proper class of topological spaces which is closed under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic to X possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets.
In general topology and related areas of mathematics, the final topology on a set with respect to a family of functions from topological spaces into is the finest topology on that makes all those functions continuous.
In topology and related fields of mathematics, a sequential space is a topological space whose topology can be completely characterized by its convergent/divergent sequences. They can be thought of as spaces that satisfy a very weak axiom of countability, and all first-countable spaces are sequential.

In topology and other branches of mathematics, a topological space X is locally connected if every point admits a neighbourhood basis consisting of open connected sets.
In topology and related areas of mathematics, a subset A of a topological space X is said to be dense in X if every point of X either belongs to A or else is arbitrarily "close" to a member of A — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it. Formally, is dense in if the smallest closed subset of containing is itself.
In the field of topology, a Fréchet–Urysohn space is a topological space with the property that for every subset the closure of in is identical to the sequential closure of in Fréchet–Urysohn spaces are a special type of sequential space.