Table of coordination geometries
A table of the coordination geometries encountered is shown below with examples of their occurrence in complexes found as discrete units in compounds and coordination spheres around atoms in crystals (where there is no discrete complex).
| Coordination number | Geometry | Examples of discrete (finite) complex | Examples in crystals (infinite solids) | |
|---|---|---|---|---|
| 2 | linear | | [Ag(CN)2]− in K[Ag(CN)2] [3] | Ag in silver cyanide, Au in AuI [2] |
| 3 | trigonal planar |  | [HgI3]− [2] | O in TiO2 rutile structure [3] |
| 4 | tetrahedral |  | [CoCl4]2− [2] | Zn and S in zinc sulfide, Si in silicon dioxide [3] |
| 4 | square planar | 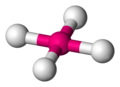 | [AgF4]− [2] | CuO [3] |
| 5 | trigonal bipyramidal |  | [SnCl5]− [3] | |
| 5 | square pyramidal | 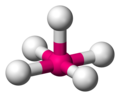 | [InCl5]2− in [N(CH2CH3)4]2[InCl5] [2] | |
| 6 | octahedral |  | [Fe(H2O)6]2+ [2] | Na and Cl in NaCl [3] |
| 6 | trigonal prismatic |  | W(CH3)6 [4] | As in NiAs, Mo in MoS2 [3] |
| 7 | pentagonal bipyramidal |  | [ZrF7]3− in [NH4]3[ZrF7] [3] | Pa in PaCl5 |
| 7 | capped octahedral |  | [MoF7]− [5] | La in A-La2O3 |
| 7 | capped trigonal prismatic |  | [TaF7]2− in K2[TaF7] [3] | |
| 8 | square antiprismatic |  | [TaF8]3− in Na3[TaF8] [3] [Zr(H2O)8]4+ aqua complex [6] | Thorium(IV) iodide [3] |
| 8 | dodecahedral (note: whilst this is the term generally used, the correct term is "bisdisphenoid" [3] or "snub disphenoid" as this polyhedron is a deltahedron) |  | [Mo(CN)8]4− in K4[Mo(CN)8]·2H2O [3] | Zr in K2[ZrF6] [3] |
| 8 | bicapped trigonal prismatic |  | [ZrF8]4− [7] | PuBr3 [3] |
| 8 | cubic | [PaF8]3− in Na3PaF8 [8] | Caesium chloride, calcium fluoride | |
| 8 | hexagonal bipyramidal | 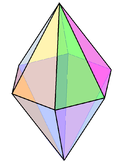 | N in Li3N [3] | |
| 8 | octahedral, trans-bicapped | Ni in nickel arsenide, NiAs; 6 As neighbours + 2 Ni capping [9] | ||
| 8 | trigonal prismatic, triangular face bicapped | Ca in CaFe2O4 [3] | ||
| 9 | tricapped trigonal prismatic |  | [ReH9]2− in potassium nonahydridorhenate [2] [Th(H2O)9]4+ aqua complex [6] | SrCl2·6H2O, Th in Rb[Th3F13] [3] |
| 9 | capped square antiprismatic |  | [Th(tropolonate)4(H2O)] [2] [ clarification needed ] | La in LaTe2 [3] |
| 10 | bicapped square antiprismatic | [Th(C2O4)4]2− [2] | ||
| 10 | bicapped cubic | Th in Th(C2O4)2·6H2O [10] | ||
| 11 | Th in [ThIV(NO3)4(H2O)3] ([NO3]− is bidentate) [2] | |||
| 12 | icosahedron |  | Th in [Th(NO3)6]2− ion in Mg[Th(NO3)6]·8H2O [3] | |
| 12 | cuboctahedron |  | ZrIV(η3-[BH4]4) | atoms in fcc metals e.g. Ca [3] |
| 12 | anticuboctahedron (triangular orthobicupola) | 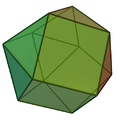 | atoms in hcp metals e.g. Sc [3] | |
| 12 | bicapped hexagonal antiprismatic | U[BH4]4 [2] |