 | This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(September 2023) |
Degree of curve or degree of curvature is a measure of curvature of a circular arc used in civil engineering for its easy use in layout surveying.
The degree of curvature is defined as the central angle to the ends of an agreed length of either an arc or a chord; [1] various lengths are commonly used in different areas of practice. This angle is also the change in forward direction as that portion of the curve is traveled. In an n-degree curve, the forward bearing changes by n degrees over the standard length of arc or chord.
Curvature is usually measured in radius of curvature. A small circle can be easily laid out by just using radius of curvature, but degree of curvature is more convenient for calculating and laying out the curve if the radius is as large as a kilometer or mile, as is needed for large scale works like roads and railroads. By using degrees of curvature, curve setting can be easily done with the help of a transit or theodolite and a chain, tape, or rope of a prescribed length.
The usual distance used to compute degree of curvature in North American road work is 100 feet (30.5 m) of arc. [2] [ page needed ] Conversely, North American railroad work traditionally used 100 feet of chord, which is used in other places[ where? ] for road work. Other lengths may be used—such as 100 metres (330 ft) where SI is favoured or a shorter length for sharper curves. Where degree of curvature is based on 100 units of arc length, the conversion between degree of curvature and radius is Dr = 18000/π ≈ 5729.57795, where D is degree and r is radius.
Since rail routes have very large radii, they are laid out in chords, as the difference to the arc is inconsequential; this made work easier before electronic calculators became available.
The 100 feet (30.48 m) is called a station, used to define length along a road or other alignment, annotated as stations plus feet 1+00, 2+00, etc. Metric work may use similar notation, such as kilometers plus meters 1+000.
Degree of curvature can be converted to radius of curvature by the following formulae:
where is arc length, is radius of curvature, and is degree of curvature, arc definition
Substitute deflection angle for degree of curvature or make arc length equal to 100 feet.
where is chord length, is radius of curvature and is degree of curvature, chord definition
As an example, a curve with an arc length of 600 units that has an overall sweep of 6 degrees is a 1-degree curve: For every 100 feet of arc, the bearing changes by 1 degree. The radius of such a curve is 5729.57795. If the chord definition is used, each 100-unit chord length will sweep 1 degree with a radius of 5729.651 units, and the chord of the whole curve will be slightly shorter than 600 units.
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc.
A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless SI derived unit, defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as rad = m/m. Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing.
A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law, where a, b, and c are the lengths of the sides of a triangle, and α, β, and γ are the opposite angles, while R is the radius of the triangle's circumcircle. When the last part of the equation is not used, the law is sometimes stated using the reciprocals; The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the triangle is not uniquely determined by this data and the technique gives two possible values for the enclosed angle.
A Fermat's spiral or parabolic spiral is a plane curve with the property that the area between any two consecutive full turns around the spiral is invariant. As a result, the distance between turns grows in inverse proportion to their distance from the spiral center, contrasting with the Archimedean spiral and the logarithmic spiral. Fermat spirals are named after Pierre de Fermat.
The great-circle distance, orthodromic distance, or spherical distance is the distance between two points on a sphere, measured along the great-circle arc between them. This arc is the shortest path between the two points on the surface of the sphere.
In geometry, a circular segment or disk segment is a region of a disk which is "cut off" from the rest of the disk by a straight line. The complete line is known as a secant, and the section inside the disk as a chord.
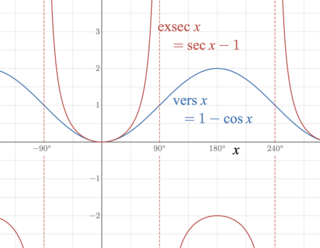
The external secant function is a trigonometric function defined in terms of the secant function:
An osculating circle is a circle that best approximates the curvature of a curve at a specific point. It is tangent to the curve at that point and has the same curvature as the curve at that point. The osculating circle provides a way to understand the local behavior of a curve and is commonly used in differential geometry and calculus.
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.
A circular sector, also known as circle sector or disk sector or simply a sector, is the portion of a disk enclosed by two radii and an arc, with the smaller area being known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle, the radius of the circle, and is the arc length of the minor sector.
Rankine's method or tangential angle method is an angular technique for laying out circular curves by a combination of chaining and angles at circumference, fully exploiting the theodolite and making a substantial improvement in accuracy and productivity over existing methods. This method requires access to only one road/path of communication to lay out a curve. Points on curve are calculated by their angular offset from the path of communication.
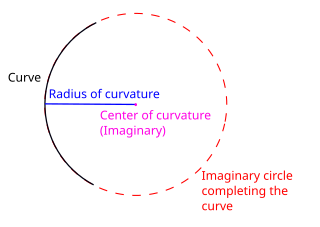
In differential geometry, the radius of curvature, R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.
In geometry, the sagitta of a circular arc is the distance from the midpoint of the arc to the midpoint of its chord. It is used extensively in architecture when calculating the arc necessary to span a certain height and distance and also in optics where it is used to find the depth of a spherical mirror or lens. The name comes directly from Latin sagitta, meaning an "arrow".
Track geometry is concerned with the properties and relations of points, lines, curves, and surfaces in the three-dimensional positioning of railroad track. The term is also applied to measurements used in design, construction and maintenance of track. Track geometry involves standards, speed limits and other regulations in the areas of track gauge, alignment, elevation, curvature and track surface. Standards are usually separately expressed for horizontal and vertical layouts although track geometry is three-dimensional.
The cant of a railway track or camber of a road is the rate of change in elevation (height) between the two rails or edges of the road. This is normally greater where the railway or road is curved; raising the outer rail or the outer edge of the road creates a banked turn, thus allowing vehicles to travel round the curve at greater speeds than would be possible if the surface were level.
| This article includes a list of general references, but it lacks sufficient corresponding inline citations .(June 2021) |
