
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the Euclidean plane. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.

In vector calculus and physics, a vector field is an assignment of a vector to each point in a subset of space. For instance, a vector field in the plane can be visualised as a collection of arrows with a given magnitude and direction, each attached to a point in the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout space, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.
In mathematics, a quadric or quadric surface, is a generalization of conic sections. It is a hypersurface in a (D + 1)-dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in D + 1 variables. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a degenerate quadric or a reducible quadric.

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
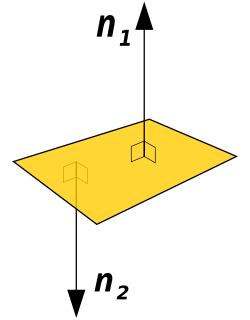
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point. A normal vector may have length one or its length may represent the curvature of the object ; its algebraic sign may indicate sides.

In mathematical physics, Minkowski space is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity.

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of positive-definiteness is relaxed.
In mathematics, conformal geometry is the study of the set of angle-preserving (conformal) transformations on a space.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.
In geometry, a striking feature of projective planes is the symmetry of the roles played by points and lines in the definitions and theorems, and (plane) duality is the formalization of this concept. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.
In mathematics, specifically linear algebra, a degenerate bilinear formf (x, y ) on a vector space V is a bilinear form such that the map from V to V∗ given by v ↦ is not an isomorphism. An equivalent definition when V is finite-dimensional is that it has a non-trivial kernel: there exist some non-zero x in V such that
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance of a vector from the origin is a norm, called the Euclidean norm, or 2-norm, which may also be defined as the square root of the inner product of a vector with itself.
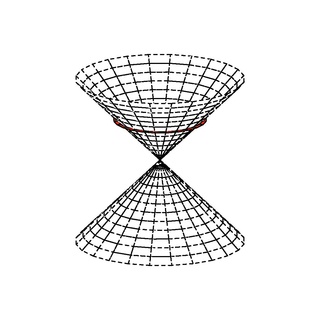
In mathematics, given a vector space X with an associated quadratic form q, written (X, q), a null vector or isotropic vector is a non-zero element x of X for which q(x) = 0.

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.
In mathematics, a quadratic form over a field F is said to be isotropic if there is a non-zero vector on which the form evaluates to zero. Otherwise the quadratic form is anisotropic. More precisely, if q is a quadratic form on a vector space V over F, then a non-zero vector v in V is said to be isotropic if q(v) = 0. A quadratic form is isotropic if and only if there exists a non-zero isotropic vector for that quadratic form.
In mathematics and theoretical physics, a pseudo-Euclidean space is a finite-dimensional real n-space together with a non-degenerate quadratic form q. Such a quadratic form can, given a suitable choice of basis (e1, …, en), be applied to a vector x = x1e1 + ⋯ + xnen, giving

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines should be regarded as circles of infinite radius and that points in the plane should be regarded as circles of zero radius.
In mathematics and physics, a vector is an element of a vector space. For many specific vector spaces, the vectors have received specific names, which are listed below. In general, a Euclidean vector is a geometric object with both length and direction, which is frequently represented as an arrow which starting point is arbitrary and thus chosen for convenience. Such vectors can be added to each other or scaled using vector algebra. Correspondingly, an ensemble of vectors is called a vector space. These objects are the subject of linear algebra and can be characterized by their dimension.














