
Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".

In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.

The Koch snowflake is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a Continuous Curve Without Tangents, Constructible from Elementary Geometry" by the Swedish mathematician Helge von Koch.

In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that the curve travels counterclockwise around the point, i.e., the curve's number of turns. For certain open plane curves, the number of turns may be a non-integer. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise.

In mathematics, a curve is an object similar to a line, but that does not have to be straight.

In mathematics, a multivalued function is a function that has two or more values in its range for at least one point in its domain. It is a set-valued function with additional properties depending on context. The terms multifunction and many-valued function are sometimes also used.

A sine wave, sinusoidal wave, or sinusoid is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is simple harmonic motion; as rotation, it corresponds to uniform circular motion. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes.
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular and equilateral. Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

In geometry, a circular segment or disk segment is a region of a disk which is "cut off" from the rest of the disk by a straight line. The complete line is known as a secant, and the section inside the disk as a chord.

In radio and telecommunications a dipole antenna or doublet is one of the two simplest and most widely-used types of antenna; the other is the monopole. The dipole is any one of a class of antennas producing a radiation pattern approximating that of an elementary electric dipole with a radiating structure supporting a line current so energized that the current has only one node at each far end. A dipole antenna commonly consists of two identical conductive elements such as metal wires or rods. The driving current from the transmitter is applied, or for receiving antennas the output signal to the receiver is taken, between the two halves of the antenna. Each side of the feedline to the transmitter or receiver is connected to one of the conductors. This contrasts with a monopole antenna, which consists of a single rod or conductor with one side of the feedline connected to it, and the other side connected to some type of ground. A common example of a dipole is the rabbit ears television antenna found on broadcast television sets. All dipoles are electrically equivalent to two monopoles mounted end-to-end and fed with opposite phases, with the ground plane between them made virtual by the opposing monopole.

In geometry, a cupola is a solid formed by joining two polygons, one with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively.

In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over its domain.

Arc length is the distance between two points along a section of a curve.
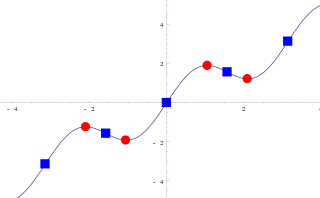
In mathematics, a critical point is the argument of a function where the function derivative is zero . The value of the function at a critical point is a critical value.

In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.
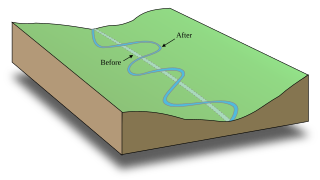
A meander is one of a series of regular sinuous curves in the channel of a river or other watercourse. It is produced as a watercourse erodes the sediments of an outer, concave bank and deposits sediments on an inner, convex bank which is typically a point bar. The result of this coupled erosion and sedimentation is the formation of a sinuous course as the channel migrates back and forth across the axis of a floodplain.

In mathematics, a complex logarithm is a generalization of the natural logarithm to nonzero complex numbers. The term refers to one of the following, which are strongly related:
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve. The theorem is a generalization of the second fundamental theorem of calculus to any curve in a plane or space rather than just the real line.

In algebraic geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.











































