A bedform is a geological feature that develops at the interface of fluid and a moveable bed, the result of bed material being moved by fluid flow. Examples include ripples and dunes on the bed of a river. Bedforms are often preserved in the rock record as a result of being present in a depositional setting. Bedforms are often characteristic to the flow parameters, [1] and may be used to infer flow depth and velocity, and therefore the Froude number.
Bedforms are omnipresent in many environments (e.g., fluvial, eolian, glaciofluvial, deltaic and deep sea), although there is still some debate on how they develop. There are two separate, though not mutually exclusive, [2] models of bedform initiation: defect initiation and instantaneous initiation.
The defect theory proposes that the turbulent sweeps that are generated in turbulent flows [3] [4] entrain sediment [5] that upon deposition generates defects in a non-cohesive material. These deposits then propagate downstream via a flow separation process, thus developing bedform fields. The origin of the defects is thought to be linked to packets of hairpin vortex structures. [6] These coherent turbulent structures give rise to entrainment corridors on the mobile bed, forming grain lineations that interact with the low-speed streaks generating an agglomeration of grains. Once a critical height of grains is reached, flow separation occurs over the new structure. Sediment will be eroded close from the reattachment point and deposited downstream creating a new defect. This new defect will thus induce formation of another defect and the process will continue, propagating downstream while the accumulations of grains quickly evolve into small bedforms.
In general, the defect propagation theory plays a bigger role at low sediment transport rates since for high rates defects maybe washed away and bedforms generally initiated across the entire bed spontaneously. [7] [8] Venditti et al. (2005) [7] : 1 report that instantaneous initiation begins with the formation of a cross-hatch pattern, which leads to chevron-shaped forms that migrate independently of the pattern structure. This chevron-like structure reorganizes to form the future crest lines of the bedforms. Venditti et al. (2006), [8] : 1 based on the earlier model by Liu (1957), proposed that instantaneous initiation is a manifestation of an interfacial hydrodynamic instability of Kelvin-Helmholtz type between a highly active pseudofluid sediment layer and the fluid above it. In addition, Venditti et al. (2005) [7] : 2 imply that there is no linkage between the instantaneous initiation and coherent turbulent flow structures, since spatially- and temporally-random events should lock in place to generate the cross-hatch pattern. Moreover, there is no clear explanation of the effect of turbulence in the formation of bedforms since bedforms may also occur under laminar flows. It is important to note, that laminar-generated bedform studies used the temporally-averaged flow conditions to determine the degree of turbulence, indicating Reynolds number in the laminar regime. However, instantaneous process, such as burst and sweeps, which are infrequent at low Reynolds number but still present, can be the driving mechanisms to generate the bedforms. The generation of bedforms in laminar flows is still a topic of debate within the scientific community, since if true, it suggests that there should be other processes for defect development other than the one suggested by Best (1992). [6] : 1 This alternative model for bedform development at low sediment transport rates should explain the generation of defects and bedforms for cases where the flow is not turbulent.
Phase or stability diagrams are defined as graphs that show the regimes of existence of one or more stable bed states. The stability of the bed can be defined when the bedform is in equilibrium and does not change in time for the same flow condition. This invariance over time must not be confused with a static morphology or frozen equilibrium; on the contrary, the bed moves and adjusts in a dynamic equilibrium with the flow and sediment transport for that particular condition. These phase diagrams [1] : 1 [9] are used for two main purposes: i) for prediction of bed states in a known flow and sediment transport condition, and, ii) as a tool for the reconstruction of paleoenvironments from a known bed state or sedimentary structure. Despite the great utility of such diagrams, they are very difficult to construct, making them either incomplete or very hard to interpret. This complexity lies in the number of variables needed to quantify the system.
Typical unidirectional bedforms represent a specific flow velocity, assuming typical sediments (sands and silts) and water depths, and a chart such as below can be used for interpreting depositional environments, [10] with increasing water velocity going down the chart.
| Flow Regime | Bedform | Preservation Potential | Identification Tips |
|---|---|---|---|
| Lower | |||
| Lower plane bed | High | Flat laminae, almost lack of current | |
| Ripple marks | High | Small, cm-scale undulations | |
| Sand waves | Medium to low | Rare, longer wavelength than ripples | |
| Dunes/Megaripples | High | Large, meter-scale ripples | |
| Upper | |||
| Upper plane bed | High | Flat laminae, +/- aligned grains (parting lineations) | |
| Antidunes | Low | Water in phase with bedform, low angle, subtle laminae | |
| Pool and chute | Very low | Mostly erosional features | |
This chart is for general use, because changes in grain size and flow depth can change the bedform present and skip bedforms in certain scenarios. Bidirectional environments (e.g. tidal flats) produce similar bedforms, but the reworking the sediments and opposite directions of flow complicates the structures.
This bed form sequence can also be illustrated diagrammatically:
"Lower plane bed" refers to the flat configuration the bed of a river that is produced in via low rates of sediment transport. [11]
"Upper plane bed" features are flat and characterized by a unidirectional flow with high rates of sediment transport as both bed load and suspended load. Upper plane bed conditions can produce parting current lineations, which are typically subtle streaks on the bed surface due to the high energy flow. [11]
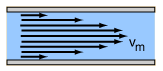
Laminar flow is the property of fluid particles in fluid dynamics to follow smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another smoothly. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In laminar flow, the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface. Laminar flow is a flow regime characterized by high momentum diffusion and low momentum convection.
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to laminar flow, which occurs when a fluid flows in parallel layers with no disruption between those layers.
In geography and geology, fluvial sediment processes or fluvial sediment transport are associated with rivers and streams and the deposits and landforms created by sediments. It can result in the formation of ripples and dunes, in fractal-shaped patterns of erosion, in complex patterns of natural river systems, and in the development of floodplains and the occurrence of flash floods. Sediment moved by water can be larger than sediment moved by air because water has both a higher density and viscosity. In typical rivers the largest carried sediment is of sand and gravel size, but larger floods can carry cobbles and even boulders. When the stream or rivers are associated with glaciers, ice sheets, or ice caps, the term glaciofluvial or fluvioglacial is used, as in periglacial flows and glacial lake outburst floods. Fluvial sediment processes include the motion of sediment and erosion or deposition on the river bed.
Deposition is the geological process in which sediments, soil and rocks are added to a landform or landmass. Wind, ice, water, and gravity transport previously weathered surface material, which, at the loss of enough kinetic energy in the fluid, is deposited, building up layers of sediment.
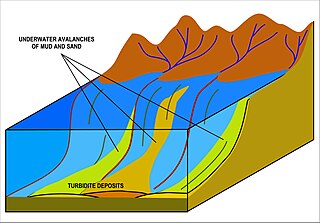
A turbidity current is most typically an underwater current of usually rapidly moving, sediment-laden water moving down a slope; although current research (2018) indicates that water-saturated sediment may be the primary actor in the process. Turbidity currents can also occur in other fluids besides water.
In fluid dynamics, the Schmidt number of a fluid is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975).
In hydrodynamics, a plume or a column is a vertical body of one fluid moving through another. Several effects control the motion of the fluid, including momentum (inertia), diffusion and buoyancy. Pure jets and pure plumes define flows that are driven entirely by momentum and buoyancy effects, respectively. Flows between these two limits are usually described as forced plumes or buoyant jets. "Buoyancy is defined as being positive" when, in the absence of other forces or initial motion, the entering fluid would tend to rise. Situations where the density of the plume fluid is greater than its surroundings, but the flow has sufficient initial momentum to carry it some distance vertically, are described as being negatively buoyant.
Entrainment is the transport of fluid across an interface between two bodies of fluid by a shear-induced turbulent flux. Entrainment is important in turbulent jets, plumes, and gravity currents, and is an ongoing topic of research.
In fluid dynamics, an eddy is the swirling of a fluid and the reverse current created when the fluid is in a turbulent flow regime. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object. Fluid behind the obstacle flows into the void creating a swirl of fluid on each edge of the obstacle, followed by a short reverse flow of fluid behind the obstacle flowing upstream, toward the back of the obstacle. This phenomenon is naturally observed behind large emergent rocks in swift-flowing rivers.
In fluid dynamics, the law of the wall states that the average velocity of a turbulent flow at a certain point is proportional to the logarithm of the distance from that point to the "wall", or the boundary of the fluid region. This law of the wall was first published in 1930 by Hungarian-American mathematician, aerospace engineer, and physicist Theodore von Kármán. It is only technically applicable to parts of the flow that are close to the wall, though it is a good approximation for the entire velocity profile of natural streams.
In geology, cross-bedding, also known as cross-stratification, is layering within a stratum and at an angle to the main bedding plane. The sedimentary structures which result are roughly horizontal units composed of inclined layers. The original depositional layering is tilted, such tilting not being the result of post-depositional deformation. Cross-beds or "sets" are the groups of inclined layers, which are known as cross-strata.
Sediment transport is the movement of solid particles (sediment), typically due to a combination of gravity acting on the sediment, and the movement of the fluid in which the sediment is entrained. Sediment transport occurs in natural systems where the particles are clastic rocks, mud, or clay; the fluid is air, water, or ice; and the force of gravity acts to move the particles along the sloping surface on which they are resting. Sediment transport due to fluid motion occurs in rivers, oceans, lakes, seas, and other bodies of water due to currents and tides. Transport is also caused by glaciers as they flow, and on terrestrial surfaces under the influence of wind. Sediment transport due only to gravity can occur on sloping surfaces in general, including hillslopes, scarps, cliffs, and the continental shelf—continental slope boundary.
The suspended load of a flow of fluid, such as a river, is the portion of its sediment uplifted by the fluid's flow in the process of sediment transportation. It is kept suspended by the fluid's turbulence. The suspended load generally consists of smaller particles, like clay, silt, and fine sands.
In fluid mechanics, pipe flow is a type of fluid flow within a closed conduit, such as a pipe, duct or tube. It is also called as Internal flow. The other type of flow within a conduit is open channel flow. These two types of flow are similar in many ways, but differ in one important aspect. Pipe flow does not have a free surface which is found in open-channel flow. Pipe flow, being confined within closed conduit, does not exert direct atmospheric pressure, but does exert hydraulic pressure on the conduit.
In fluid dynamics, the Reynolds number is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers, flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow. These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation.
In hydrology stream competency, also known as stream competence, is a measure of the maximum size of particles a stream can transport. The particles are made up of grain sizes ranging from large to small and include boulders, rocks, pebbles, sand, silt, and clay. These particles make up the bed load of the stream. Stream competence was originally simplified by the “sixth-power-law,” which states the mass of a particle that can be moved is proportional to the velocity of the river raised to the sixth power. This refers to the stream bed velocity which is difficult to measure or estimate due to the many factors that cause slight variances in stream velocities.
A sediment gravity flow is one of several types of sediment transport mechanisms, of which most geologists recognize four principal processes. These flows are differentiated by their dominant sediment support mechanisms, which can be difficult to distinguish as flows can be in transition from one type to the next as they evolve downslope.
Subhasish Dey is a hydraulician and educator. He is known for his research on the hydrodynamics and acclaimed for his contributions in developing theories and solution methodologies of various problems on applied hydrodynamics, river mechanics, sediment dynamics, turbulence, fluid boundary layer and open channel flow. He is currently a distinguished professor of Indian Institute of Technology Jodhpur (2023–). Before, he worked as a professor of the department of civil engineering, Indian Institute of Technology Kharagpur (1998–2023), where he served as the head of the department during 2013–15 and held the position of Brahmaputra Chair Professor during 2009–14 and 2015. He also held the adjunct professor position in the Physics and Applied Mathematics Unit at Indian Statistical Institute Kolkata during 2014–19. Besides he has been named a distinguished visiting professor at the Tsinghua University in Beijing, China.
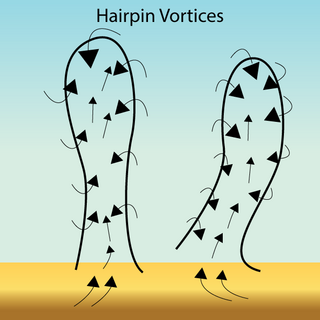
Turbulent flows are complex multi-scale and chaotic motions that need to be classified into more elementary components, referred to coherent turbulent structures. Such a structure must have temporal coherence, i.e. it must persist in its form for long enough periods that the methods of time-averaged statistics can be applied. Coherent structures are typically studied on very large scales, but can be broken down into more elementary structures with coherent properties of their own, such examples include hairpin vortices. Hairpins and coherent structures have been studied and noticed in data since the 1930s, and have been since cited in thousands of scientific papers and reviews.
Multiscale turbulence is a class of turbulent flows in which the chaotic motion of the fluid is forced at different length and/or time scales. This is usually achieved by immersing in a moving fluid a body with a multiscale, often fractal-like, arrangement of length scales. This arrangement of scales can be either passive or active
| Large-scale features | |
|---|---|
| Alluvial rivers | |
| Bedrock river | |
| Bedforms | |
| Regional processes | |
| Mechanics | |
