
A self-organizing map (SOM) or self-organizing feature map (SOFM) is an unsupervised machine learning technique used to produce a low-dimensional representation of a higher-dimensional data set while preserving the topological structure of the data. For example, a data set with variables measured in observations could be represented as clusters of observations with similar values for the variables. These clusters then could be visualized as a two-dimensional "map" such that observations in proximal clusters have more similar values than observations in distal clusters. This can make high-dimensional data easier to visualize and analyze.
In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.

An artificial neuron is a mathematical function conceived as a model of a biological neuron in a neural network. The artificial neuron is the elementary unit of an artificial neural network.
A Hopfield network is a form of recurrent neural network, or a spin glass system, that can serve as a content-addressable memory. The Hopfield network, named for John Hopfield, consists of a single layer of neurons, where each neuron is connected to every other neuron except itself. These connections are bidirectional and symmetric, meaning the weight of the connection from neuron i to neuron j is the same as the weight from neuron j to neuron i. Patterns are associatively recalled by fixing certain inputs, and dynamically evolve the network to minimize an energy function, towards local energy minimum states that correspond to stored patterns. Patterns are associatively learned by a Hebbian learning algorithm.
In machine learning, backpropagation is a gradient estimation method commonly used for training a neural network to compute its parameter updates.
Winner-take-all is a computational principle applied in computational models of neural networks by which neurons compete with each other for activation. In the classical form, only the neuron with the highest activation stays active while all other neurons shut down; however, other variations allow more than one neuron to be active, for example the soft winner take-all, by which a power function is applied to the neurons.
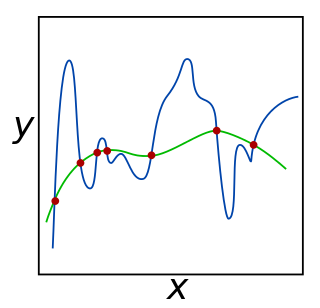
In mathematics, statistics, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the answer of a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting.
Neural coding is a neuroscience field concerned with characterising the hypothetical relationship between the stimulus and the neuronal responses, and the relationship among the electrical activities of the neurons in the ensemble. Based on the theory that sensory and other information is represented in the brain by networks of neurons, it is believed that neurons can encode both digital and analog information.

An autoencoder is a type of artificial neural network used to learn efficient codings of unlabeled data. An autoencoder learns two functions: an encoding function that transforms the input data, and a decoding function that recreates the input data from the encoded representation. The autoencoder learns an efficient representation (encoding) for a set of data, typically for dimensionality reduction, to generate lower-dimensional embeddings for subsequent use by other machine learning algorithms.
Oja's learning rule, or simply Oja's rule, named after Finnish computer scientist Erkki Oja, is a model of how neurons in the brain or in artificial neural networks change connection strength, or learn, over time. It is a modification of the standard Hebb's Rule that, through multiplicative normalization, solves all stability problems and generates an algorithm for principal components analysis. This is a computational form of an effect which is believed to happen in biological neurons.
Hierarchical temporal memory (HTM) is a biologically constrained machine intelligence technology developed by Numenta. Originally described in the 2004 book On Intelligence by Jeff Hawkins with Sandra Blakeslee, HTM is primarily used today for anomaly detection in streaming data. The technology is based on neuroscience and the physiology and interaction of pyramidal neurons in the neocortex of the mammalian brain.
The generalized Hebbian algorithm, also known in the literature as Sanger's rule, is a linear feedforward neural network for unsupervised learning with applications primarily in principal components analysis. First defined in 1989, it is similar to Oja's rule in its formulation and stability, except it can be applied to networks with multiple outputs. The name originates because of the similarity between the algorithm and a hypothesis made by Donald Hebb about the way in which synaptic strengths in the brain are modified in response to experience, i.e., that changes are proportional to the correlation between the firing of pre- and post-synaptic neurons.

Biological neuron models, also known as spiking neuron models, are mathematical descriptions of the conduction of electrical signals in neurons. Neurons are electrically excitable cells within the nervous system, able to fire electric signals, called action potentials, across a neural network. These mathematical models describe the role of the biophysical and geometrical characteristics of neurons on the conduction of electrical activity.
In neuroethology and the study of learning, anti-Hebbian learning describes a particular class of learning rule by which synaptic plasticity can be controlled. These rules are based on a reversal of Hebb's postulate, and therefore can be simplistically understood as dictating reduction of the strength of synaptic connectivity between neurons following a scenario in which a neuron directly contributes to production of an action potential in another neuron.
Bidirectional associative memory (BAM) is a type of recurrent neural network. BAM was introduced by Bart Kosko in 1988. There are two types of associative memory, auto-associative and hetero-associative. BAM is hetero-associative, meaning given a pattern it can return another pattern which is potentially of a different size. It is similar to the Hopfield network in that they are both forms of associative memory. However, Hopfield nets return patterns of the same size.
Competitive learning is a form of unsupervised learning in artificial neural networks, in which nodes compete for the right to respond to a subset of the input data. A variant of Hebbian learning, competitive learning works by increasing the specialization of each node in the network. It is well suited to finding clusters within data.
There are many types of artificial neural networks (ANN).
An attractor network is a type of recurrent dynamical network, that evolves toward a stable pattern over time. Nodes in the attractor network converge toward a pattern that may either be fixed-point, cyclic, chaotic or random (stochastic). Attractor networks have largely been used in computational neuroscience to model neuronal processes such as associative memory and motor behavior, as well as in biologically inspired methods of machine learning.
RAMnets is one of the oldest practical neurally inspired classification algorithms. The RAMnets is also known as a type of "n-tuple recognition method" or "weightless neural network".
The spike response model (SRM) is a spiking neuron model in which spikes are generated by either a deterministic or a stochastic threshold process. In the SRM, the membrane voltage V is described as a linear sum of the postsynaptic potentials (PSPs) caused by spike arrivals to which the effects of refractoriness and adaptation are added. The threshold is either fixed or dynamic. In the latter case it increases after each spike. The SRM is flexible enough to account for a variety of neuronal firing pattern in response to step current input. The SRM has also been used in the theory of computation to quantify the capacity of spiking neural networks; and in the neurosciences to predict the subthreshold voltage and the firing times of cortical neurons during stimulation with a time-dependent current stimulation. The name Spike Response Model points to the property that the two important filters and of the model can be interpreted as the response of the membrane potential to an incoming spike (response kernel , the PSP) and to an outgoing spike (response kernel , also called refractory kernel). The SRM has been formulated in continuous time and in discrete time. The SRM can be viewed as a generalized linear model (GLM) or as an (integrated version of) a generalized integrate-and-fire model with adaptation.
















































