Volume (thermodynamics)

Volume (thermodynamics)
Volume (thermodynamics)
Common symbols	V
SI unit	m 3

Last updated April 21, 2024

In thermodynamics, the volume of a system is an important extensive parameter for describing its thermodynamic state. The specific volume , an intensive property, is the system's volume per unit mass. Volume is a function of state and is interdependent with other thermodynamic properties such as pressure and temperature. For example, volume is related to the pressure and temperature of an ideal gas by the ideal gas law. The physical region covered by a system may or may not coincide with a control volume used to analyze the system.

Overview

The volume of a thermodynamic system typically refers to the volume of the working fluid, such as, for example, the fluid within a piston. Changes to this volume may be made through an application of work, or may be used to produce work. An isochoric process however operates at a constant-volume, thus no work can be produced. Many other thermodynamic processes will result in a change in volume. A polytropic process, in particular, causes changes to the system so that the quantity $pV^{n}$ is constant (where $p$ is pressure, $V$ is volume, and $n$ is the polytropic index, a constant). Note that for specific polytropic indexes, a polytropic process will be equivalent to a constant-property process. For instance, for very large values of $n$ approaching infinity, the process becomes constant-volume.

Gases are compressible, thus their volumes (and specific volumes) may be subject to change during thermodynamic processes. Liquids, however, are nearly incompressible, thus their volumes can be often taken as constant. In general, compressibility is defined as the relative volume change of a fluid or solid as a response to a pressure, and may be determined for substances in any phase. Similarly, thermal expansion is the tendency of matter to change in volume in response to a change in temperature.

Many thermodynamic cycles are made up of varying processes, some which maintain a constant volume and some which do not. A vapor-compression refrigeration cycle, for example, follows a sequence where the refrigerant fluid transitions between the liquid and vapor states of matter.

Typical units for volume are $\mathrm {m^{3}}$ (cubic meters), $\mathrm {l}$ (liters), and $\mathrm {ft} ^{3}$ (cubic feet).

Heat and work

Mechanical work performed on a working fluid causes a change in the mechanical constraints of the system; in other words, for work to occur, the volume must be altered. Hence, volume is an important parameter in characterizing many thermodynamic processes where an exchange of energy in the form of work is involved.

Volume is one of a pair of conjugate variables, the other being pressure. As with all conjugate pairs, the product is a form of energy. The product $pV$ is the energy lost to a system due to mechanical work. This product is one term which makes up enthalpy $H$ :

H=U+pV,\,

where $U$ is the internal energy of the system.

The second law of thermodynamics describes constraints on the amount of useful work which can be extracted from a thermodynamic system. In thermodynamic systems where the temperature and volume are held constant, the measure of "useful" work attainable is the Helmholtz free energy; and in systems where the volume is not held constant, the measure of useful work attainable is the Gibbs free energy.

Similarly, the appropriate value of heat capacity to use in a given process depends on whether the process produces a change in volume. The heat capacity is a function of the amount of heat added to a system. In the case of a constant-volume process, all the heat affects the internal energy of the system (i.e., there is no pV-work, and all the heat affects the temperature). However, in a process without a constant volume, the heat addition affects both the internal energy and the work (i.e., the enthalpy); thus the temperature changes by a different amount than in the constant-volume case and a different heat capacity value is required.

Specific volume

Specific volume ( $\nu$ ) is the volume occupied by a unit of mass of a material.^[1] In many cases, the specific volume is a useful quantity to determine because, as an intensive property, it can be used to determine the complete state of a system in conjunction with another independent intensive variable. The specific volume also allows systems to be studied without reference to an exact operating volume, which may not be known (nor significant) at some stages of analysis.

The specific volume of a substance is equal to the reciprocal of its mass density. Specific volume may be expressed in ${\frac {\mathrm {m^{3}} }{\mathrm {kg} }}$ , ${\frac {\mathrm {ft^{3}} }{\mathrm {lb} }}$ , ${\frac {\mathrm {ft^{3}} }{\mathrm {slug} }}$ , or ${\frac {\mathrm {mL} }{\mathrm {g} }}$ .

\nu ={\frac {V}{m}}={\frac {1}{\rho }}

where, $V$ is the volume, $m$ is the mass and $\rho$ is the density of the material.

For an ideal gas,

\nu ={\frac {{\bar {R}}T}{P}}

where, ${\bar {R}}$ is the specific gas constant, $T$ is the temperature and $P$ is the pressure of the gas.

Specific volume may also refer to molar volume.

Gas volume

Dependence on pressure and temperature

The volume of gas increases proportionally to absolute temperature and decreases inversely proportionally to pressure, approximately according to the ideal gas law:

V={\frac {nRT}{p}}

where:

p is the pressure
V is the volume
n is the amount of substance of gas (moles)
R is the gas constant, 8.314 J·K ⁻¹ mol ⁻¹
T is the absolute temperature

To simplify, a volume of gas may be expressed as the volume it would have in standard conditions for temperature and pressure, which are 0 °C (32 °F) and 100 kPa.^[2]

Humidity exclusion

In contrast to other gas components, water content in air, or humidity, to a higher degree depends on vaporization and condensation from or into water, which, in turn, mainly depends on temperature. Therefore, when applying more pressure to a gas saturated with water, all components will initially decrease in volume approximately according to the ideal gas law. However, some of the water will condense until returning to almost the same humidity as before, giving the resulting total volume deviating from what the ideal gas law predicted. Conversely, decreasing temperature would also make some water condense, again making the final volume deviating from predicted by the ideal gas law.

Therefore, gas volume may alternatively be expressed excluding the humidity content: V_d (volume dry). This fraction more accurately follows the ideal gas law. On the contrary, V_s (volume saturated) is the volume a gas mixture would have if humidity was added to it until saturation (or 100% relative humidity).

General conversion

To compare gas volume between two conditions of different temperature or pressure (1 and 2), assuming nR are the same, the following equation uses humidity exclusion in addition to the ideal gas law:

V_{2}=V_{1}\times {\frac {T_{2}}{T_{1}}}\times {\frac {p_{1}-p_{w,1}}{p_{2}-p_{w,2}}}

Where, in addition to terms used in the ideal gas law:

p_w is the partial pressure of gaseous water during condition 1 and 2, respectively

For example, calculating how much 1 liter of air (a) at 0 °C, 100 kPa, p_w = 0 kPa (known as STPD, see below) would fill when breathed into the lungs where it is mixed with water vapor (l), where it quickly becomes 37 °C (99 °F), 100 kPa, p_w = 6.2 kPa (BTPS):

V_{l}=1\ \mathrm {l} \times {\frac {310\ \mathrm {K} }{273\ \mathrm {K} }}\times {\frac {100\ \mathrm {kPa} -0\ \mathrm {kPa} }{100\ \mathrm {kPa} -6.2\ \mathrm {kPa} }}=1.21\ \mathrm {l}

Common conditions

Some common expressions of gas volume with defined or variable temperature, pressure and humidity inclusion are:

ATPS: Ambient temperature (variable) and pressure (variable), saturated (humidity depends on temperature)
ATPD: Ambient temperature (variable) and pressure (variable), dry (no humidity)
BTPS: Body temperature (37 °C or 310 K) and pressure (generally same as ambient), saturated (47 mmHg or 6.2 kPa)
STPD: Standard temperature (0 °C or 273 K) and pressure (760 mmHg (101.33 kPa) or 100 kPa (750.06 mmHg)), dry (no humidity)

Conversion factors

The following conversion factors can be used to convert between expressions for volume of a gas:^[3]

To convert from	To	Multiply by
ATPS	STPD	[(P_A – P_{water S}) / P_S] * [T_S / T_A]
	BTPS	[(P_A – P_{water S}) / (P_A – P_{water B})] * [T_B/T_A]
	ATPD	(P_A – P_{water S}) / P_A
ATPD	STPD	(P_A / P_S) * (T_S / T_A)
	BTPS	[P_A / (P_A – P_{water B})] * (T_B / T_A)
	ATPS	P_A / (P_A – P_{water S})
BTPS	STPD	[(P_A – P_{water B}) / P_S] * [T_S / T_B]
	ATPS	[(P_A – P_{water B}) / (P_A – P_{water S})] * [T_A / T_B]
	ATPD	[(P_A – P_{water B}) / P_A] * [T_A / T_B]
STPD	BTPS	[P_S / (P_A - P_{water B})] * [T_B / T_S]
	ATPS	[P_S / (P_A - P_{water S})] * [T_A / T_S]
	ATPD	[P_S / P_A] * [T_A / T_S]
Legend: P_A = Ambient pressure P_S = Standard pressure (100 kPa or 750 mmHg) P_{water S} = Partial pressure of water in saturated air (that is, at 100% relative humidity; in this case the partial pressure is equal to the vapour pressure, which can be determined as a function of ambient temperature) P_{water B} = Partial pressure of water in saturated air in 37 °C = 47 mmHg T_S = Standard temperature in kelvins (K) = 273 K T_A = Ambient temperature in kelvins = 273 + t (where t is ambient temperature in °C) T_B = Body temperature in kelvins = 310 K

Partial volume

The partial volume of a particular gas is a fraction of the total volume occupied by the gas mixture, with unchanged pressure and temperature. In gas mixtures, e.g. air, the partial volume allows focusing on one particular gas component, e.g. oxygen.

It can be approximated both from partial pressure and molar fraction:^[4]

V_{\rm {X}}=V_{\rm {tot}}\times {\frac {P_{\rm {X}}}{P_{\rm {tot}}}}=V_{\rm {tot}}\times {\frac {n_{\rm {X}}}{n_{\rm {tot}}}}

V_X is the partial volume of any individual gas component (X)
V_tot is the total volume in gas mixture
P_X is the partial pressure of gas X
P_tot is the total pressure in gas mixture
n_X is the amount of substance of a gas (X)
n_tot is the total amount of substance in gas mixture

Related Research Articles

An adiabatic process is a type of thermodynamic process that occurs without transferring heat or mass between the thermodynamic system and its environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work. As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics.

In thermodynamics, enthalpy, is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant external pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work $that was done against constant external pressure to establish the system's physical dimensions from to some final volume, i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; bond, lattice, solvation, and other chemical "energies" are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it.$

In thermodynamics, the specific heat capacity of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat capacity or as the specific heat. More formally it is the heat capacity of a sample of the substance divided by the mass of the sample. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg⁻¹⋅K⁻¹. For example, the heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules, so the specific heat capacity of water is 4184 J⋅kg⁻¹⋅K⁻¹.

In a mixture of gases, each constituent gas has a partial pressure which is the notional pressure of that constituent gas as if it alone occupied the entire volume of the original mixture at the same temperature. The total pressure of an ideal gas mixture is the sum of the partial pressures of the gases in the mixture.

The molar gas constant is denoted by the symbol $R$ or $R$ . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, rather than energy per temperature increment per particle. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.

In chemistry and related fields, the molar volume, symbol V_m, or $of a substance is the ratio of the volume occupied by a substance to the amount of substance, usually given at a given temperature and pressure. It is equal to the molar mass (M) divided by the mass density (ρ):$

In thermodynamics, the Joule–Thomson effect describes the temperature change of a real gas or liquid when it is forced through a valve or porous plug while keeping it insulated so that no heat is exchanged with the environment. This procedure is called a throttling process or Joule–Thomson process. At room temperature, all gases except hydrogen, helium, and neon cool upon expansion by the Joule–Thomson process when being throttled through an orifice; these three gases experience the same effect but only at lower temperatures. Most liquids such as hydraulic oils will be warmed by the Joule–Thomson throttling process.

<span class="mw-page-title-main">Fermi gas</span> Physical model of gases composed of many non-interacting identical fermions

A Fermi gas is an idealized model, an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as

In physical chemistry, Henry's law is a gas law that states that the amount of dissolved gas in a liquid is directly proportional to its partial pressure above the liquid. The proportionality factor is called Henry's law constant. It was formulated by the English chemist William Henry, who studied the topic in the early 19th century. In simple words, we can say that the partial pressure of a gas in vapour phase is directly proportional to the mole fraction of a gas in solution.

The internal energy of a thermodynamic system is the energy contained within it, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accounting for the gains and losses of energy due to changes in its internal state, including such quantities as magnetization. It excludes the kinetic energy of motion of the system as a whole and the potential energy of position of the system as a whole, with respect to its surroundings and external force fields. It includes the thermal energy, i.e., the constituent particles' kinetic energies of motion relative to the motion of the system as a whole. The internal energy of an isolated system cannot change, as expressed in the law of conservation of energy, a foundation of the first law of thermodynamics.

In thermodynamics, an isochoric process, also called a constant-volume process, an isovolumetric process, or an isometric process, is a thermodynamic process during which the volume of the closed system undergoing such a process remains constant. An isochoric process is exemplified by the heating or the cooling of the contents of a sealed, inelastic container: The thermodynamic process is the addition or removal of heat; the isolation of the contents of the container establishes the closed system; and the inability of the container to deform imposes the constant-volume condition.

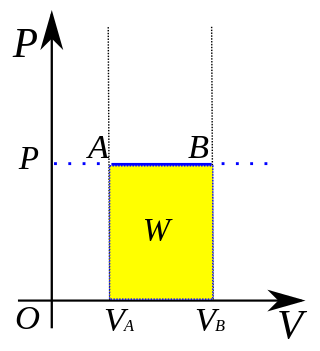
In thermodynamics, an isobaric process is a type of thermodynamic process in which the pressure of the system stays constant: ΔP = 0. The heat transferred to the system does work, but also changes the internal energy (U) of the system. This article uses the physics sign convention for work, where positive work is work done by the system. Using this convention, by the first law of thermodynamics,

The density of air or atmospheric density, denoted ρ, is the mass per unit volume of Earth's atmosphere. Air density, like air pressure, decreases with increasing altitude. It also changes with variations in atmospheric pressure, temperature and humidity. At 101.325 kPa (abs) and 20 °C, air has a density of approximately 1.204 kg/m³ (0.0752 lb/cu ft), according to the International Standard Atmosphere (ISA). At 101.325 kPa (abs) and 15 °C (59 °F), air has a density of approximately 1.225 kg/m³ (0.0765 lb/cu ft), which is about 1⁄800 that of water, according to the International Standard Atmosphere (ISA). Pure liquid water is 1,000 kg/m³ (62 lb/cu ft).

In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it cannot exchange energy or particles with its environment, so that the energy of the system does not change with time.

Thermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics.

The Clausius–Clapeyron relation, in chemical thermodynamics, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. It's named after Rudolf Clausius and Benoît Paul Émile Clapeyron. However, this relation was in fact originally derived by Sadi Carnot in his Reflections on the Motive Power of Fire, which was published in 1824 but largely ignored until it was rediscovered by Clausius, Clapeyron, and Lord Kelvin decades later. Kelvin said of Carnot's argument that "nothing in the whole range of Natural Philosophy is more remarkable than the establishment of general laws by such a process of reasoning."

A thermodynamic cycle consists of linked sequences of thermodynamic processes that involve transfer of heat and work into and out of the system, while varying pressure, temperature, and other state variables within the system, and that eventually returns the system to its initial state. In the process of passing through a cycle, the working fluid (system) may convert heat from a warm source into useful work, and dispose of the remaining heat to a cold sink, thereby acting as a heat engine. Conversely, the cycle may be reversed and use work to move heat from a cold source and transfer it to a warm sink thereby acting as a heat pump. If at every point in the cycle the system is in thermodynamic equilibrium, the cycle is reversible. Whether carried out reversible or irreversibly, the net entropy change of the system is zero, as entropy is a state function.

A polytropic process is a thermodynamic process that obeys the relation:

References

↑ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach . Boston: McGraw-Hill. pp. 11. ISBN 0-07-238332-1.
↑ A. D. McNaught, A. Wilkinson (1997). Compendium of Chemical Terminology, The Gold Book (2nd ed.). Blackwell Science. ISBN 0-86542-684-8.
↑ Brown, Stanle y; Miller, Wayne; Eason, M (2006). Exercise Physiology: Basis of Human Movement in Health and Disease. Lippincott Williams & Wilkins. p. 113. ISBN 0-7817-3592-0 . Retrieved 13 February 2014.
↑ Page 200 in: Medical biophysics. Flemming Cornelius. 6th Edition, 2008.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach . Boston: McGraw-Hill. pp. 11. ISBN 0-07-238332-1.

[IUPAC-2] A. D. McNaught, A. Wilkinson (1997). Compendium of Chemical Terminology, The Gold Book (2nd ed.). Blackwell Science. ISBN 0-86542-684-8.

[3] Brown, Stanle y; Miller, Wayne; Eason, M (2006). Exercise Physiology: Basis of Human Movement in Health and Disease. Lippincott Williams & Wilkins. p. 113. ISBN 0-7817-3592-0 . Retrieved 13 February 2014.

[biophysics200-4] Page 200 in: Medical biophysics. Flemming Cornelius. 6th Edition, 2008.

[1]

[2]

[3]

[4]

v t e Mole concepts
Constants	Avogadro constant Boltzmann constant Gas constant
Physical quantities	Mass concentration Molar concentration Molality Mass Volume Density Mole fraction Mass fraction Amount of substance Molar mass Atomic mass Particle number Pressure Thermodynamic temperature Molar volume Specific volume
Laws	Charles's law Boyle's law Gay-Lussac's law Combined gas law Avogadro's law Ideal gas law