
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609, describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in the heliocentric theory of Nicolaus Copernicus with elliptical orbits and explained how planetary velocities vary. The three laws state that:
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

In celestial mechanics, the Lagrange points are points of equilibrium for small-mass objects under the gravitational influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem.

In celestial mechanics, escape velocity or escape speed is the minimum speed needed for an object to escape from contact with or orbit of a primary body, assuming:

An apsis is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides is the line connecting the two extreme values.
The orbital period is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.
In gravitationally bound systems, the orbital speed of an astronomical body or object is the speed at which it orbits around either the barycenter or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body.
The astronomical system of units, formerly called the IAU (1976) System of Astronomical Constants, is a system of measurement developed for use in astronomy. It was adopted by the International Astronomical Union (IAU) in 1976 via Resolution No. 1, and has been significantly updated in 1994 and 2009.

The Hill sphere is a common model for the calculation of a gravitational sphere of influence. It is the most commonly used model to calculate the spatial extent of gravitational influence of an astronomical body (m) in which it dominates over the gravitational influence of other bodies, particularly a primary (M). It is sometimes confused with other models of gravitational influence, such as the Laplace sphere or being named the Roche sphere, the latter causing confusion with the Roche limit. It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche.

Comet NEAT, formally designated as C/2002 V1, is a non-periodic comet that appeared in November 2002. The comet peaked with an apparent magnitude of approximately –0.5, making it the eighth-brightest comet seen since 1935. It was seen by SOHO in February 2003. At perihelion the comet was only 0.0992 AU (14.84 million km) from the Sun, where it was initially expected to be disintegrated, however reanalysis of its orbit has indicated that it has survived many of its previous perihelia, thus making breakup unlikely.

The Jupiter mass, also called Jovian mass, is the unit of mass equal to the total mass of the planet Jupiter. This value may refer to the mass of the planet alone, or the mass of the entire Jovian system to include the moons of Jupiter. Jupiter is by far the most massive planet in the Solar System. It is approximately 2.5 times as massive as all of the other planets in the Solar System combined.
C/2007 W1 (Boattini) is a non-periodic comet discovered on 20 November 2007, by Andrea Boattini at the Mt. Lemmon Survey. At the peak the comet had an apparent magnitude around 5.
The Heliocentric Julian Date (HJD) is the Julian Date (JD) corrected for differences in the Earth's position with respect to the Sun. When timing events that occur beyond the Solar System, due to the finite speed of light, the time the event is observed depends on the changing position of the observer in the Solar System. Before multiple observations can be combined, they must be reduced to a common, fixed, reference location. This correction also depends on the direction to the object or event being timed.
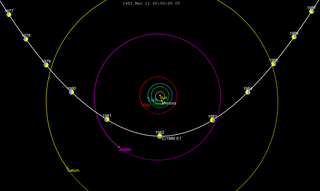
C/1980 E1 is a non-periodic comet discovered by Edward L. G. Bowell on 11 February 1980 and which came closest to the Sun (perihelion) in March 1982. It is leaving the Solar System on a hyperbolic trajectory due to a close approach to Jupiter. In the 43 years since its discovery only two objects with higher eccentricities have been identified, 1I/ʻOumuamua (1.2) and 2I/Borisov (3.35).
The Barycentric Julian Date (BJD) is the Julian Date (JD) corrected for differences in the Earth's position with respect to the barycentre of the Solar System. Due to the finite speed of light, the time an astronomical event is observed depends on the changing position of the observer in the Solar System. Before multiple observations can be combined, they must be reduced to a common, fixed, reference location. This correction also depends on the direction to the object or event being timed.
The tug of war in astronomy is the ratio of planetary and solar attractions on a natural satellite. The term was coined by Isaac Asimov in The Magazine of Fantasy and Science Fiction in 1963.

C/1999 S4 (LINEAR) was a hyperbolic comet discovered by the Lincoln Near-Earth Asteroid Research survey on 27 September 1999.

C/2013 US10 (Catalina) is an Oort cloud comet discovered on 31 October 2013 by the Catalina Sky Survey at an apparent magnitude of 19 using a 0.68-meter (27 in) Schmidt–Cassegrain telescope. From September 2015 to February 2016 the comet was around apparent magnitude 6. The comet took around a million years to complete half an orbit from its furthest distance in the Oort cloud and should be ejected from the Solar System over many millions of years.
2010 BK118 (also written 2010 BK118) is a centaur roughly 20–60 km in diameter. It is on a retrograde cometary orbit. It has a barycentric semi-major axis (average distance from the Sun) of ~400 AU.

2014 FE72 is a trans-Neptunian object first observed on 26 March 2014, at Cerro Tololo Inter-American Observatory in La Serena, Chile. It is a possible dwarf planet, a member of the scattered disc, whose orbit extends into the inner Oort cloud. Discovered by Scott Sheppard and Chad Trujillo, the object's existence was revealed on 29 August 2016. Both the orbital period and aphelion distance of this object are well constrained. 2014 FE72 had the largest barycentric aphelion until 2018. However, the heliocentric aphelion of 2014 FE72 is second among trans-Neptunian objects (after the damocloid 2017 MB7). As of 2023, it is about 66 AU (9.9 billion km) from the Sun.





















