In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit (i.e. an elliptic or other conic one) that it would have around its central body if perturbations were absent. [1] That is, it is the orbit that coincides with the current orbital state vectors (position and velocity).
The word osculate is Latin for "kiss". In mathematics, two curves osculate when they just touch, without (necessarily) crossing, at a point, where both have the same position and slope, i.e. the two curves "kiss".
An osculating orbit and the object's position upon it can be fully described by the six standard Kepler orbital elements (osculating elements), which are easy to calculate as long as one knows the object's position and velocity relative to the central body. The osculating elements would remain constant in the absence of perturbations. Real astronomical orbits experience perturbations that cause the osculating elements to evolve, sometimes very quickly. In cases where general celestial mechanical analyses of the motion have been carried out (as they have been for the major planets, the Moon, and other planetary satellites), the orbit can be described by a set of mean elements with secular and periodic terms. In the case of minor planets, a system of proper orbital elements has been devised to enable representation of the most important aspects of their orbits.
Perturbations that cause an object's osculating orbit to change can arise from:
An object's orbital parameters will be different if they are expressed with respect to a non-inertial reference frame (for example, a frame co-precessing with the primary's equator), than if it is expressed with respect to a (non-rotating) inertial reference frame.
Put in more general terms, a perturbed trajectory can be analysed as if assembled of points, each of which is contributed by a curve out of a sequence of curves. Variables parameterising the curves within this family can be called orbital elements . Typically (though not necessarily), these curves are chosen as Keplerian conics, all of which share one focus. In most situations, it is convenient to set each of these curves tangent to the trajectory at the point of intersection. Curves that obey this condition (and also the further condition that they have the same curvature at the point of tangency as would be produced by the object's gravity towards the central body in the absence of perturbing forces) are called osculating, while the variables parameterising these curves are called osculating elements. In some situations, description of orbital motion can be simplified and approximated by choosing orbital elements that are not osculating. Also, in some situations, the standard (Lagrange-type or Delaunay-type) equations furnish orbital elements that turn out to be non-osculating. [2]
In celestial mechanics, the Lagrange points are points of equilibrium for small-mass objects under the gravitational influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem.
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes, each consisting of a set of six parameters, are commonly used in astronomy and orbital mechanics.
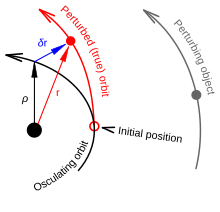
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter . The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction.
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics to astronomical objects, such as stars and planets, to produce ephemeris data.
The orbital period is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
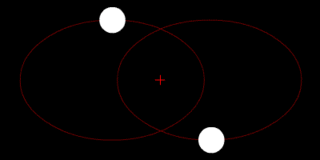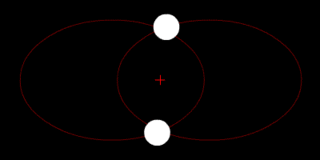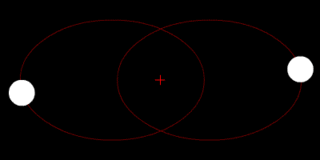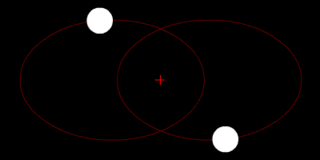
In astronomy, the barycenter is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit. A barycenter is a dynamical point, not a physical object. It is an important concept in fields such as astronomy and astrophysics. The distance from a body's center of mass to the barycenter can be calculated as a two-body problem.
A Klemperer rosette is a gravitational system of (optionally) alternating heavier and lighter bodies orbiting in a symmetrical pattern around a common barycenter. It was first described by W.B. Klemperer in 1962, and is a special case of a central configuration.
The Laplace plane or Laplacian plane of a planetary satellite, named after its discoverer Pierre-Simon Laplace (1749–1827), is a mean or reference plane about whose axis the instantaneous orbital plane of that satellite precesses.
In astrodynamics and celestial dynamics, the orbital state vectors of an orbit are Cartesian vectors of position and velocity that together with their time (epoch) uniquely determine the trajectory of the orbiting body in space.
A sphere of influence (SOI) in astrodynamics and astronomy is the oblate-spheroid-shaped region around a celestial body where the primary gravitational influence on an orbiting object is that body. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as moons, despite the presence of the much more massive but distant Sun. In the patched conic approximation, used in estimating the trajectories of bodies moving between the neighbourhoods of different masses using a two body approximation, ellipses and hyperbolae, the SOI is taken as the boundary where the trajectory switches which mass field it is influenced by.
JPL Horizons On-Line Ephemeris System provides access to key Solar System data and flexible production of highly accurate ephemerides for Solar System objects.
In astronomy, perturbation is the complex motion of a massive body subjected to forces other than the gravitational attraction of a single other massive body. The other forces can include a third body, resistance, as from an atmosphere, and the off-center attraction of an oblate or otherwise misshapen body.
The proper orbital elements or proper elements of an orbit are constants of motion of an object in space that remain practically unchanged over an astronomically long timescale. The term is usually used to describe the three quantities:
Tisserand's parameter is a value calculated from several orbital elements of a relatively small object and a larger "perturbing body". It is used to distinguish different kinds of orbits. The term is named after French astronomer Félix Tisserand, and applies to restricted three-body problems in which the three objects all differ greatly in mass.
The two-body problem in general relativity is the determination of the motion and gravitational field of two bodies as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet orbiting its sun. Solutions are also used to describe the motion of binary stars around each other, and estimate their gradual loss of energy through gravitational radiation.
In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.
Orbit modeling is the process of creating mathematical models to simulate motion of a massive body as it moves in orbit around another massive body due to gravity. Other forces such as gravitational attraction from tertiary bodies, air resistance, solar pressure, or thrust from a propulsion system are typically modeled as secondary effects. Directly modeling an orbit can push the limits of machine precision due to the need to model small perturbations to very large orbits. Because of this, perturbation methods are often used to model the orbit in order to achieve better accuracy.
Gravitational orbits | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Types |
| ||||||||
| Parameters |
| ||||||||
| Maneuvers | |||||||||
| Orbital mechanics |
| ||||||||
