
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

In celestial mechanics, escape velocity or escape speed is the minimum speed needed for an object to escape from contact with or orbit of a primary body, assuming:

In astronautics, the Hohmann transfer orbit is an orbital maneuver used to transfer a spacecraft between two orbits of different altitudes around a central body. For example, a Hohmann transfer could be used to raise a satellite's orbit from low Earth orbit to geostationary orbit. In the idealized case, the initial and target orbits are both circular and coplanar. The maneuver is accomplished by placing the craft into an elliptical transfer orbit that is tangential to both the initial and target orbits. The maneuver uses two impulsive engine burns: the first establishes the transfer orbit, and the second adjusts the orbit to match the target.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets, satellites, and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
In gravitationally bound systems, the orbital speed of an astronomical body or object is the speed at which it orbits around either the barycenter or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body.
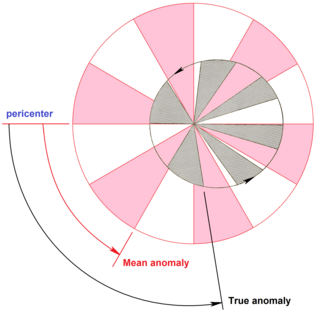
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical two-body problem. It is the angular distance from the pericenter which a fictitious body would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual body in its elliptical orbit.

In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away from the source it is called an escape orbit, otherwise a capture orbit. It is also sometimes referred to as a C3 = 0 orbit (see Characteristic energy).
The standard gravitational parameterμ of a celestial body is the product of the gravitational constant G and the mass M of that body. For two bodies, the parameter may be expressed as G(m1 + m2), or as GM when one body is much larger than the other:

In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.
In astrodynamics, the characteristic energy is a measure of the excess specific energy over that required to just barely escape from a massive body. The units are length2 time−2, i.e. velocity squared, or energy per mass.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1. They are frequently used during various astrodynamic calculations.
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version.
In the gravitational two-body problem, the specific orbital energy of two orbiting bodies is the constant sum of their mutual potential energy and their kinetic energy, divided by the reduced mass. According to the orbital energy conservation equation, it does not vary with time: where
In astrodynamics, the vis-viva equation, also referred to as orbital-energy-invariance law or Burgas formula, is one of the equations that model the motion of orbiting bodies. It is the direct result of the principle of conservation of mechanical energy which applies when the only force acting on an object is its own weight which is the gravitational force determined by the product of the mass of the object and the strength of the surrounding gravitational field.

In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit, and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

In astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer maneuver.

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.

In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle.
In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.













































