Extended discrete element method

Last updated
An internal temperature distribution for a spherical particle versus radius and time under a time-varying heat flux. Internal temperature distribution in a particle.png
An internal temperature distribution for a spherical particle versus radius and time under a time-varying heat flux.

The extended discrete element method (XDEM) is a numerical technique that extends the dynamics of granular material or particles as described through the classical discrete element method (DEM) (Cundall [1] and Allen [2] ) by additional properties such as the thermodynamic state, stress/strain or electro-magnetic field for each particle. Contrary to a continuum mechanics concept, the XDEM aims at resolving the particulate phase with its various processes attached to the particles. While the discrete element method predicts position and orientation in space and time for each particle, the extended discrete element method additionally estimates properties such as internal temperature and/or species distribution or mechanical impact with structures.

Contents

History

Molecular dynamics developed in the late 1950s by Alder et al. [3] and early 1960s by Rahman [4] may be regarded as a first step toward the extended discrete element method, although the forces due to collisions between particles were replaced by energy potentials e.g. Lennard-Jones potentials of molecules and atoms as long range forces to determine interaction.

Similarly, the fluid dynamic interaction of particles suspended in a flow were investigated. The drag forces exerted on the particles by the relative velocity by them and the flow were treated as additional forces acting on the particles. Therefore, these multiphase flow phenomena including a solid e.g.~particulate and a gaseous or fluid phase resolve the particulate phase by discrete methods, while gas or liquid flow is described by continuous methods, and therefore, is labelled the combined continuum and discrete model (CCDM) as applied by Kawaguchi et al., [5] Hoomans, [6] Xu 1997 [7] and Xu 1998. [8] Due to a discrete description of the solid phase, constitutive relations are omitted, and therefore, leads to a better understanding of the fundamentals. This was also concluded by Zhu 2007 et al. [9] and Zhu 2008 et al. [10] during a review on particulate flows modelled with the CCDM approach. It has seen a mayor development in last two decades and describes motion of the solid phase by the Discrete Element Method (DEM) on an individual particle scale and the remaining phases are treated by the Navier-Stokes equations. Thus, the method is recognized as an effective tool to investigate into the interaction between a particulate and fluid phase as reviewed by Yu and Xu, [11] Feng and Yu [12] and Deen et al. [13] Based on the CCDM methodology the characteristics of spouted and fluidised beds are predicted by Gryczka et al. [14]

The theoretical foundation for the XDEM was developed in 1999 by Peters, [15] who described incineration of a wooden moving bed on a forward acting grate. [16] The concept was later also employed by Sismsek et al. [17] to predict the furnace process of a grate firing system. Applications to the complex processes of a blast furnace have been attempted by Shungo et al. [18] Numerical simulation of fluid injection into a gaseous environment nowadays is adopted by a large number of CFD-codes such as Simcenter STAR-CCM+, Ansys and AVL-Fire. Droplets of a spray are treated by a zero-dimensional approach to account for heat and mass transfer to the fluid phase.

Methodology

Staggered methodology for discrete/continuous applications. Staggered methodology for software coupling.png
Staggered methodology for discrete/continuous applications.

Many engineering problems exist that include continuous and discrete phases, and those problems cannot be simulated accurately by continuous or discrete approaches. XDEM provides a solution for some of those engineering applications.

Although research and development of numerical methods in each domains of discrete and continuous solvers is still progressing, software tools are available. In order to couple discrete and continuous approaches, two major approaches are available:

The former approach requires a solver that handles all physical problems involved, therefore it requires a larger implementation effort. However, there exist scenarios for which it is difficult to arrange the coefficients of combined differential equations in one matrix.

The latter, partitioned, approach couples a number of solvers representing individual domains of physics offers advantages over a monolithic concept. It encompasses a larger degree of flexibility because it can use many solvers. Furthermore, it allows a more modular software development. However, partitioned simulations require stable and accurate coupling algorithms.

Within the staggered concept of XDEM, continuous fields are described by the solution the respective continuous (conservation) equations. Properties of individual particles such as temperature are also resolved by solving respective conservation equations that yield both a spatial and temporal internal distribution of relevant variables. Major conservation principles with their equations and variables to be solved for and that are employed to an individual particle within XDEM are listed in the following table.

Conservation principles of Interfaces
Conservation law Equation Variable
Mass (compressible medium)ContinuityPressure/density
Linear Momentum Navier-Stokes Velocity
Energy EnergyTemperature
Species massSpecies transportMass fractions
Charge, current Maxwell electric, magnetic field, electric displacement field

The solution of these equations in principle defines a three-dimensional and transient field of the relevant variables such as temperature or species. However, the application of these conservation principles to a large number of particles usually restricts the resolution to at most one representative dimension and time due to CPU time consumption. Experimental evidence at least in reaction engineering supports the assumption of one-dimensionality as pointed out by Man and Byeong, [19] while the importance of a transient behaviour is stressed by Lee et al. [20]

Applications

Deformation of a conveyor belt due to impacting granular material. Particles impacting on a conveyer belt.png
Deformation of a conveyor belt due to impacting granular material.

Problems that involve both a continuous and a discrete phase are important in applications as diverse as pharmaceutical industry e.g.~drug production, agriculture food and processing industry, mining, construction and agricultural machinery, metals manufacturing, energy production and systems biology. Some predominant examples are coffee, corn flakes, nuts, coal, sand, renewable fuels e.g.~biomass for energy production and fertilizer.

Initially, such studies were limited to simple flow configurations as pointed out by Hoomans, [21] however, Chu and Yu [22] demonstrated that the method could be applied to a complex flow configuration consisting of a fluidized bed, conveyor belt and a cyclone. Similarly, Zhou et al. [23] applied the CCDM approach to the complex geometry of fuel-rich/lean burner for pulverised coal combustion in a plant and Chu et al. [24] modelled the complex flow of air, water, coal and magnetite particles of different sizes in a dense medium cyclone (DMC).

The CCDM approach has also been applied to fluidised beds as reviewed by Rowe and Nienow [25] and Feng and Yu [26] and applied by Feng and Yu [27] to the chaotic motion of particles of different sizes in a gas fluidized bed. Kafuia et al. [28] describe discrete particle-continuum fluid modelling of gas-solid fluidised beds. Further applications of XDEM include thermal conversion of biomass on a backward and forward acting grate. Heat transfer in thermal/reacting particulate systems was also solved and investigated, as comprehensively reviewed by Peng et al. [29] The deformation of a conveyor belt due to impacting granular material that is discharged over a chute represents an application in the field of stress/strain analysis.

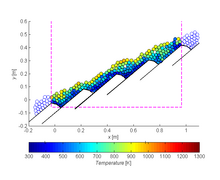
Distribution of particles' surface temperature on a backward acting grate. Temperature distribution on a backward acting grate.png
Distribution of particles' surface temperature on a backward acting grate.
Progress of pyrolysis of straw blades on a forward acting grate, on which straw is converted into charred material Char distribution on a forward acting grate.png
Progress of pyrolysis of straw blades on a forward acting grate, on which straw is converted into charred material
Distribution of porosity inside the packed bed and particle temperature Particle temperature in a packed bed reactor.png
Distribution of porosity inside the packed bed and particle temperature

Related Research Articles

A discrete element method (DEM), also called a distinct element method, is any of a family of numerical methods for computing the motion and effect of a large number of small particles. Though DEM is very closely related to molecular dynamics, the method is generally distinguished by its inclusion of rotational degrees-of-freedom as well as stateful contact and often complicated geometries. With advances in computing power and numerical algorithms for nearest neighbor sorting, it has become possible to numerically simulate millions of particles on a single processor. Today DEM is becoming widely accepted as an effective method of addressing engineering problems in granular and discontinuous materials, especially in granular flows, powder mechanics, and rock mechanics. DEM has been extended into the Extended Discrete Element Method taking heat transfer, chemical reaction and coupling to CFD and FEM into account.

<span class="mw-page-title-main">Heat transfer</span> Transport of thermal energy in physical systems

Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species, either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system.

<span class="mw-page-title-main">Computational fluid dynamics</span> Analysis and solving of problems that involve fluid flows

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.

<span class="mw-page-title-main">Level-set method</span>

Level-set methods (LSM) are a conceptual framework for using level sets as a tool for numerical analysis of surfaces and shapes. The advantage of the level-set model is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects. Also, the level-set method makes it very easy to follow shapes that change topology, for example, when a shape splits in two, develops holes, or the reverse of these operations. All these make the level-set method a great tool for modeling time-varying objects, like inflation of an airbag, or a drop of oil floating in water.

<span class="mw-page-title-main">Smoothed-particle hydrodynamics</span> Method of hydrodynamics simulation

Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and fluid flows. It was developed by Gingold and Monaghan and Lucy in 1977, initially for astrophysical problems. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography. It is a meshfree Lagrangian method, and the resolution of the method can easily be adjusted with respect to variables such as density.

<span class="mw-page-title-main">Fluidized bed</span>

A fluidized bed is a physical phenomenon that occurs when a solid particulate substance is under the right conditions so that it behaves like a fluid. The usual way to achieve a fluidized bed is to pump pressurized fluid into the particles. The resulting medium then has many properties and characteristics of normal fluids, such as the ability to free-flow under gravity, or to be pumped using fluid technologies.

<span class="mw-page-title-main">Lattice Boltzmann methods</span> Class of computational fluid dynamics methods

The lattice Boltzmann methods (LBM), originated from the lattice gas automata (LGA) method (Hardy-Pomeau-Pazzis and Frisch-Hasslacher-Pomeau models), is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier–Stokes equations directly, a fluid density on a lattice is simulated with streaming and collision (relaxation) processes. The method is versatile as the model fluid can straightforwardly be made to mimic common fluid behaviour like vapour/liquid coexistence, and so fluid systems such as liquid droplets can be simulated. Also, fluids in complex environments such as porous media can be straightforwardly simulated, whereas with complex boundaries other CFD methods can be hard to work with.

<span class="mw-page-title-main">Multiphase flow</span>

In fluid mechanics, multiphase flow is the simultaneous flow of materials with two or more thermodynamic phases. Virtually all processing technologies from cavitating pumps and turbines to paper-making and the construction of plastics involve some form of multiphase flow. It is also prevalent in many natural phenomena.

<span class="mw-page-title-main">Fluid–structure interaction</span>

Fluid–structure interaction (FSI) is the interaction of some movable or deformable structure with an internal or surrounding fluid flow. Fluid–structure interactions can be stable or oscillatory. In oscillatory interactions, the strain induced in the solid structure causes it to move such that the source of strain is reduced, and the structure returns to its former state only for the process to repeat.

<span class="mw-page-title-main">Meshfree methods</span> Methods in numerical analysis not requiring knowledge of neighboring points

In the field of numerical analysis, meshfree methods are those that do not require connection between nodes of the simulation domain, i.e. a mesh, but are rather based on interaction of each node with all its neighbors. As a consequence, original extensive properties such as mass or kinetic energy are no longer assigned to mesh elements but rather to the single nodes. Meshfree methods enable the simulation of some otherwise difficult types of problems, at the cost of extra computing time and programming effort. The absence of a mesh allows Lagrangian simulations, in which the nodes can move according to the velocity field.

The material point method (MPM) is a numerical technique used to simulate the behavior of solids, liquids, gases, and any other continuum material. Especially, it is a robust spatial discretization method for simulating multi-phase (solid-fluid-gas) interactions. In the MPM, a continuum body is described by a number of small Lagrangian elements referred to as 'material points'. These material points are surrounded by a background mesh/grid that is used to calculate terms such as the deformation gradient. Unlike other mesh-based methods like the finite element method, finite volume method or finite difference method, the MPM is not a mesh based method and is instead categorized as a meshless/meshfree or continuum-based particle method, examples of which are smoothed particle hydrodynamics and peridynamics. Despite the presence of a background mesh, the MPM does not encounter the drawbacks of mesh-based methods which makes it a promising and powerful tool in computational mechanics.

The CFD-DEM model, or Computational Fluid Dynamics / Discrete Element Method model, is a process used to model or simulate systems combining fluids with solids or particles. In CFD-DEM, the motion of discrete solids or particles phase is obtained by the Discrete Element Method (DEM) which applies Newton's laws of motion to every particle, while the flow of continuum fluid is described by the local averaged Navier–Stokes equations that can be solved using the traditional Computational Fluid Dynamics (CFD) approach. The interactions between the fluid phase and solids phase is modeled by use of Newton's third law.

A CFD-DEM model is suitable for the modeling or simulation of fluid-solids or fluid-particles systems. In a typical CFD-DEM model, the phase motion of discrete solids or particles is obtained by the Discrete Element Method (DEM) which applies Newton's laws of motion to every particle and the flow of continuum fluid is described by the local averaged Navier–Stokes equations that can be solved by the traditional Computational Fluid Dynamics (CFD). The model is first proposed by Tsuji et al. The interactions between the fluid phase and solids phase is better modeled according to Newton's third law.

In computational fluid dynamics, the immersed boundary method originally referred to an approach developed by Charles Peskin in 1972 to simulate fluid-structure (fiber) interactions. Treating the coupling of the structure deformations and the fluid flow poses a number of challenging problems for numerical simulations. In the immersed boundary method the fluid is represented in an Eulerian coordinate system and the structure is represented in Lagrangian coordinates. For Newtonian fluids governed by the Navier–Stokes equations, the fluid equations are

Population balance equations (PBEs) have been introduced in several branches of modern science, mainly in Chemical Engineering, to describe the evolution of a population of particles. This includes topics like crystallization, leaching (metallurgy), liquid–liquid extraction, gas-liquid dispersions like water electrolysis, liquid-liquid reactions, comminution, aerosol engineering, biology (where the separate entities are cells based on their size or intracellular proteins), polymerization, etc. Population balance equations can be said to be derived as an extension of the Smoluchowski coagulation equation which describes only the coalescence of particles. PBEs, more generally, define how populations of separate entities develop in specific properties over time. They are a set of Integro-partial differential equations which gives the mean-field behavior of a population of particles from the analysis of behavior of single particle in local conditions. Particulate systems are characterized by the birth and death of particles. For example, consider precipitation process (formation of solid from liquid solution) which has the subprocesses nucleation, agglomeration, breakage, etc., that result in the increase or decrease of the number of particles of a particular radius (assuming formation of spherical particles). Population balance is nothing but a balance on the number of particles of a particular state (in this example, size).

The moving particle semi-implicit (MPS) method is a computational method for the simulation of incompressible free surface flows. It is a macroscopic, deterministic particle method developed by Koshizuka and Oka (1996).

Particle-laden flows refers to a class of two-phase fluid flow, in which one of the phases is continuously connected and the other phase is made up of small, immiscible, and typically dilute particles. Fine aerosol particles in air is an example of a particle-laden flow; the aerosols are the dispersed phase, and the air is the carrier phase.

The multiphase particle-in-cell method (MP-PIC) is a numerical method for modeling particle-fluid and particle-particle interactions in a computational fluid dynamics (CFD) calculation. The MP-PIC method achieves greater stability than its particle-in-cell predecessor by simultaneously treating the solid particles as computational particles and as a continuum. In the MP-PIC approach, the particle properties are mapped from the Lagrangian coordinates to an Eulerian grid through the use of interpolation functions. After evaluation of the continuum derivative terms, the particle properties are mapped back to the individual particles. This method has proven to be stable in dense particle flows, computationally efficient, and physically accurate. This has allowed the MP-PIC method to be used as particle-flow solver for the simulation of industrial-scale chemical processes involving particle-fluid flows.

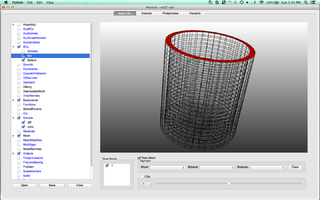
<span class="mw-page-title-main">MOOSE (software)</span>

MOOSE is an object-oriented C++ finite element framework for the development of tightly coupled multiphysics solvers from Idaho National Laboratory. MOOSE makes use of the PETSc non-linear solver package and libmesh to provide the finite element discretization.

Quadrature-based moment methods (QBMM) are a class of computational fluid dynamics (CFD) methods for solving Kinetic theory and is optimal for simulating phases such as rarefied gases or dispersed phases of a multiphase flow. The smallest "particle" entities which are tracked may be molecules of a single phase or granular "particles" such as aerosols, droplets, bubbles, precipitates, powders, dust, soot, etc. Moments of the Boltzmann equation are solved to predict the phase behavior as a continuous (Eulerian) medium, and is applicable for arbitrary Knudsen number and arbitrary Stokes number . Source terms for collision models such as Bhatnagar-Gross-Krook (BGK) and models for evaporation, coalescence, breakage, and aggregation are also available. By retaining a quadrature approximation of a probability density function (PDF), a set of abscissas and weights retain the physical solution and allow for the construction of moments that generate a set of partial differential equations (PDE's). QBMM has shown promising preliminary results for modeling granular gases or dispersed phases within carrier fluids and offers an alternative to Lagrangian methods such as Discrete Particle Simulation (DPS). The Lattice Boltzmann Method (LBM) shares some strong similarities in concept, but it relies on fixed abscissas whereas quadrature-based methods are more adaptive. Additionally, the Navier–Stokes equations(N-S) can be derived from the moment method approach.

References

  1. ↑ Cundall, P. A.; Strack, O. D. L. (1979). "A discrete numerical model for granular assemblies". Geotechnique. 29: 47–65. doi:10.1680/geot.1979.29.1.47.
  2. ↑ Allen, M. P.; Tildesley, D. J. (1990). Computer Simulation of Liquids. Clarendon Press Oxford.
  3. ↑ Alder, B. J.; Wainwright, T. E. (1959). "Studies in Molecular Dynamics. I. General Method". J. Chem. Phys. 31 (2): 459–466. Bibcode:1959JChPh..31..459A. doi:10.1063/1.1730376.
  4. ↑ Rahman, A. (1964). "Correlations in the Motion of Atoms in Liquid Argon". Phys. Rev. 136 (2A): A405–A411. Bibcode:1964PhRv..136..405R. doi:10.1103/physrev.136.a405.
  5. ↑ Kawaguchi, T.; Tsuji, Y.; Tanaka, T. (1993). "Discrete particle simulation of two-dimensional fluidized bed". Powder Technol. 77: 79–87. doi:10.1016/0032-5910(93)85010-7.
  6. ↑ Hoomans, B. P. B.; Kuipers, J. A. M.; Briels, W. J.; Van Swaaij, W. P. M. (1996). "Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed: A hard-sphere approach". Chem. Eng. Sci. 51: 99–118. CiteSeerX   10.1.1.470.6532 . doi:10.1016/0009-2509(95)00271-5. S2CID   17460834.
  7. ↑ Xu, B. H.; Yu, A. B. (1997). "Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics". Chemical Engineering Science. 52 (16): 2785–2809. doi:10.1016/s0009-2509(97)00081-x.
  8. ↑ Xu, B. H.; Yu, A. B. (1998). "Comments on the paper numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics". Chemical Engineering Science. 53 (14): 2646–2647. doi:10.1016/s0009-2509(98)00086-4.
  9. ↑ Zhu, H. P.; Zhou, Z. Y.; Yang, R. Y.; Yu, A. B. (2007). "Discrete particle simulation of particulate systems: Theoretical developments". Chemical Engineering Science. 62 (13): 3378–3396. doi:10.1016/j.ces.2006.12.089.
  10. ↑ Zhu, H. P.; Zhou, Z. Y.; Yang, R. Y.; Yu, A. B. (2008). "Discrete particle simulation of particulate systems: A review of major applications and findings". Chemical Engineering Science. 63 (23): 5728–5770. doi:10.1016/j.ces.2008.08.006.
  11. ↑ Xu, B. H.; Yu, A. B. (2003). "Particle-scale modelling of gas-solid flow in fluidisation". Journal of Chemical Technology and Biotechnology. 78 (2–3): 111–121. doi:10.1002/jctb.788.
  12. ↑ Feng, Y. Q.; Yu, A. B.; Yu, A. B.; Vince, A. (2004). "Assessment of model formulations in the discrete particle simulation of gas-solid flow". Industrial & Engineering Chemistry Research. 43 (26): 8378–8390. doi:10.1021/ie049387v.
  13. ↑ Deen, N. G.; Annaland, M. V. S.; Van Der Hoef, M. A.; Kuipers, J. A. M. (2007). "Review of discrete particle modeling of fluidized beds". Chemical Engineering Science. 62 (1–2): 28–44. doi:10.1016/j.ces.2006.08.014.
  14. ↑ Gryczka, O.; Heinrich, S.; Deen, N. S.; van Sint Annaland, M.; Kuipers, J. A. M.; Mörl, M. (2009). "CFD modeling of a prismatic spouted bed with two adjustable gas inlets". Canadian Journal of Chemical Engineering. 87 (2): 318–328. CiteSeerX   10.1.1.335.4108 . doi:10.1002/cjce.20143.
  15. ↑ Peters, B. (1999). "Classification of combustion regimes in a packed bed based on the relevant time and length scales". Combustion and Flame. 116 (1–2): 297–301. doi:10.1016/s0010-2180(98)00048-0.
  16. ↑ Peters, B. (2002). "Measurements and application of a discrete particle model (DPM) to simulate combustion of a packed bed of individual fuel particles". Combustion and Flame. 131 (1–2): 132–146. doi:10.1016/s0010-2180(02)00393-0.
  17. ↑ Simsek, E.; Brosch, B.; Wirtz, S.; Scherer, V.; Kröll, F. (2009). "Numerical simulation of grate firing systems using a coupled CFD/Discrete Element Method (DEM)". Powder Technology. 193 (3): 266–273. doi:10.1016/j.powtec.2009.03.011.
  18. ↑ Natsui, Shungo; Ueda, Shigeru; Fan, Zhengyun; Andersson, Nils; Kano, Junya; Inoue, Ryo; Ariyama, Tatsuro (2010). "Characteristics of solid flow and stress distribution including asymmetric phenomena in blast furnace analyzed by discrete element method". ISIJ International. 50 (2): 207–214. doi: 10.2355/isijinternational.50.207 .
  19. ↑ Man, Y. H.; Byeong, R. C. (1994). "A numerical study on the combustion of a single carbon particle entrained in a steady flow". Combustion and Flame. 97: 1–16. doi:10.1016/0010-2180(94)90112-0.
  20. ↑ Lee, J. C.; Yetter, R. A.; Dryer, F. L. (1996). "Numerical simulation of laser ignition of an isolated carbon particle in quiescent environment". Combustion and Flame. 105 (4): 591–599. doi:10.1016/0010-2180(96)00221-0.
  21. ↑ Hoomans, B. P. B.; Kuipers, J. A. M.; Briels, W. J.; Van Swaaij, W. P. M. (1996). "Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed: A hard-sphere approach". Chem. Eng. Sci. 51: 99–118. CiteSeerX   10.1.1.470.6532 . doi:10.1016/0009-2509(95)00271-5. S2CID   17460834.
  22. ↑ Chu, K. W.; Yu, A. B. (2008). "Numerical simulation of complex particle-fluid flows". Powder Technology. 179 (3): 104–114. doi:10.1016/j.powtec.2007.06.017.
  23. ↑ Zhou, H.; Mo, G.; Zhao, J.; Cen, K. (2011). "DEM-CFD simulation of the particle dispersion in a gas-solid two-phase flow for a fuel-rich/lean burner". Fuel. 90 (4): 1584–1590. doi:10.1016/j.fuel.2010.10.017.
  24. ↑ Chu, K. W.; Wang, B.; Yu, A. B.; Vince, A.; Barnett, G. D.; Barnett, P. J. (2009). "CFD-DEM study of the effect of particle density distribution on the multiphase flow and performance of dense medium cyclone". Minerals Engineering. 22 (11): 893–909. doi:10.1016/j.mineng.2009.04.008.
  25. ↑ Rowe, P. N.; Nienow, A. W. (1976). "Particle mixing and segregation in gas fluidized beds: A review". Powder Technology. 15 (2): 141–147. doi:10.1016/0032-5910(76)80042-3.
  26. ↑ Feng, Y. Q.; Yu, A. B.; Yu, A. B.; Vince, A. (2004). "Assessment of model formulations in the discrete particle simulation of gas-solid flow". Industrial & Engineering Chemistry Research. 43 (26): 8378–8390. doi:10.1021/ie049387v.
  27. ↑ Feng, Y. Q.; Yu, A. B. (2008). "An analysis of the chaotic motion of particles of different sizes in a gas fluidized bed". Particuology. 6 (6): 549–556. doi:10.1016/j.partic.2008.07.011.
  28. ↑ Kafuia, K. D.; Thornton, C.; Adams, M. J. (2002). "Discrete particle-continuum fluid modelling of gas-solid fluidised beds". Chemical Engineering Science. 57 (13): 2395–2410. doi:10.1016/s0009-2509(02)00140-9.
  29. ↑ Peng, Z.; Doroodchi, E.; Moghtaderi, B. (2020). "Heat transfer modelling in Discrete Element Method (DEM)-based simulations of thermal processes: Theory and model development". Progress in Energy and Combustion Science. 79, 100847: 100847. doi:10.1016/j.pecs.2020.100847. S2CID   218967044.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.