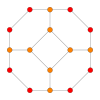
In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

In four-dimensional euclidean geometry, the tesseractic honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {4,3,3,4}, and constructed by a 4-dimensional packing of tesseract facets.

In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {3,3,4,3}, and constructed by a 4-dimensional packing of 16-cell facets, three around every face.

In ten-dimensional geometry, a 10-polytope is a 10-dimensional polytope whose boundary consists of 9-polytope facets, exactly two such facets meeting at each 8-polytope ridge.
In eight-dimensional geometry, a heptellated 8-simplex is a convex uniform 8-polytope, including 7th-order truncations (heptellation) from the regular 8-simplex.
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ratio of 1:1.
In five-dimensional Euclidean geometry, the 5-simplex honeycomb or hexateric honeycomb is a space-filling tessellation. Each vertex is shared by 12 5-simplexes, 30 rectified 5-simplexes, and 20 birectified 5-simplexes. These facet types occur in proportions of 2:2:1 respectively in the whole honeycomb.
In five-dimensional Euclidean geometry, the omnitruncated 5-simplex honeycomb or omnitruncated hexateric honeycomb is a space-filling tessellation. It is composed entirely of omnitruncated 5-simplex facets.
In six-dimensional Euclidean geometry, the 6-simplex honeycomb is a space-filling tessellation. The tessellation fills space by 6-simplex, rectified 6-simplex, and birectified 6-simplex facets. These facet types occur in proportions of 1:1:1 respectively in the whole honeycomb.
In four-dimensional Euclidean geometry, the snub 24-cell honeycomb, or snub icositetrachoric honeycomb is a uniform space-filling tessellation by snub 24-cells, 16-cells, and 5-cells. It was discovered by Thorold Gosset with his 1900 paper of semiregular polytopes. It is not semiregular by Gosset's definition of regular facets, but all of its cells (ridges) are regular, either tetrahedra or icosahedra.
In four-dimensional Euclidean geometry, the rectified 24-cell honeycomb is a uniform space-filling honeycomb. It is constructed by a rectification of the regular 24-cell honeycomb, containing tesseract and rectified 24-cell cells.

In geometry, the simplicial honeycomb is a dimensional infinite series of honeycombs, based on the affine Coxeter group symmetry. It is represented by a Coxeter-Dynkin diagram as a cyclic graph of n + 1 nodes with one node ringed. It is composed of n-simplex facets, along with all rectified n-simplices. It can be thought of as an n-dimensional hypercubic honeycomb that has been subdivided along all hyperplanes , then stretched along its main diagonal until the simplices on the ends of the hypercubes become regular. The vertex figure of an n-simplex honeycomb is an expanded n-simplex.

In geometry, the cyclotruncated simplicial honeycomb is a dimensional infinite series of honeycombs, based on the symmetry of the affine Coxeter group. It is given a Schläfli symbol t0,1{3[n+1]}, and is represented by a Coxeter-Dynkin diagram as a cyclic graph of n+1 nodes with two adjacent nodes ringed. It is composed of n-simplex facets, along with all truncated n-simplices.
In seven-dimensional Euclidean geometry, the 7-simplex honeycomb is a space-filling tessellation. The tessellation fills space by 7-simplex, rectified 7-simplex, birectified 7-simplex, and trirectified 7-simplex facets. These facet types occur in proportions of 2:2:2:1 respectively in the whole honeycomb.
In eighth-dimensional Euclidean geometry, the 8-simplex honeycomb is a space-filling tessellation. The tessellation fills space by 8-simplex, rectified 8-simplex, birectified 8-simplex, and trirectified 8-simplex facets. These facet types occur in proportions of 1:1:1:1 respectively in the whole honeycomb.
In six-dimensional Euclidean geometry, the omnitruncated 6-simplex honeycomb is a space-filling tessellation. It is composed entirely of omnitruncated 6-simplex facets.
In eight-dimensional Euclidean geometry, the omnitruncated 8-simplex honeycomb is a space-filling tessellation. It is composed entirely of omnitruncated 8-simplex facets.
In seven-dimensional Euclidean geometry, the omnitruncated 7-simplex honeycomb is a space-filling tessellation. It is composed entirely of omnitruncated 7-simplex facets.
In four-dimensional Euclidean geometry, the omnitruncated tesseractic honeycomb is a uniform space-filling honeycomb. It has omnitruncated tesseract, truncated cuboctahedral prism, and 8-8 duoprism facets in an irregular 5-cell vertex figure.
In four-dimensional Euclidean geometry, the stericantitruncated tesseractic honeycomb is a uniform space-filling honeycomb. It is composed of runcitruncated 16-cell, cantitruncated tesseract, rhombicuboctahedral prism, truncated cuboctahedral prism, and 4-8 duoprism facets, arranged around an irregular 5-cell vertex figure.