In vector calculus, the Jacobian matrix of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and the determinant are often referred to simply as the Jacobian in literature.

Atmospheric chemistry is a branch of atmospheric science in which the chemistry of the Earth's atmosphere and that of other planets is studied. It is a multidisciplinary approach of research and draws on environmental chemistry, physics, meteorology, computer modeling, oceanography, geology and volcanology and other disciplines. Research is increasingly connected with other areas of study such as climatology.
In mathematics and computer algebra, automatic differentiation, also called algorithmic differentiation, computational differentiation, is a set of techniques to evaluate the partial derivative of a function specified by a computer program.
In mathematics, the total derivative of a function f at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when f is a function of several variables, because when f is a function of a single variable, the total derivative is the same as the ordinary derivative of the function.

The Gauss–Newton algorithm is used to solve non-linear least squares problems, which is equivalent to minimizing a sum of squared function values. It is an extension of Newton's method for finding a minimum of a non-linear function. Since a sum of squares must be nonnegative, the algorithm can be viewed as using Newton's method to iteratively approximate zeroes of the components of the sum, and thus minimizing the sum. In this sense, the algorithm is also an effective method for solving overdetermined systems of equations. It has the advantage that second derivatives, which can be challenging to compute, are not required.
In mathematics, a hyperbolic partial differential equation of order is a partial differential equation (PDE) that, roughly speaking, has a well-posed initial value problem for the first derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation. In one spatial dimension, this is
A Hessian is an inhabitant of the German state of Hesse.
In mathematics, a differential-algebraic system of equations (DAE) is a system of equations that either contains differential equations and algebraic equations, or is equivalent to such a system.
In mathematics, a critical point is the argument of a function where the function derivative is zero . The value of the function at a critical point is a critical value.
In mathematics, the derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, geometry, etc.
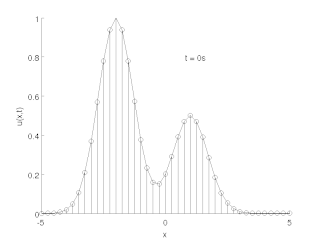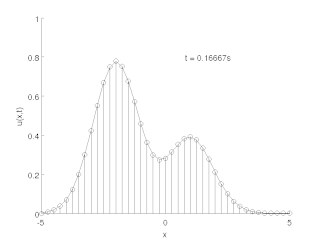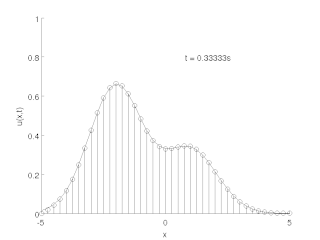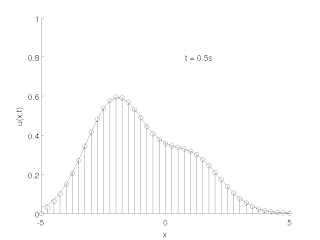
The method of lines is a technique for solving partial differential equations (PDEs) in which all but one dimension is discretized. By reducing a PDE to a single continuous dimension, the method of lines allows solutions to be computed via methods and software developed for the numerical integration of ordinary differential equations (ODEs) and differential-algebraic systems of equations (DAEs). Many integration routines have been developed over the years in many different programming languages, and some have been published as open source resources.

David J. Lary is a British-American atmospheric scientist interested in applying computational and information systems to facilitate discovery and decision support in Earth system science. His main contributions have been to highlight the role of carbonaceous aerosols in atmospheric chemistry, heterogeneous bromine reactions, and to employ chemical data assimilation for satellite validation, and the use of machine learning for remote sensing applications. He is author of AutoChem, NASA release software that constitutes an automatic computer code generator and documentor for chemically reactive systems. It was designed primarily for modeling atmospheric chemistry, and in particular, for chemical data assimilation. He is author of more than 200 publications receiving more than 6,000 citations.
The Kinetic PreProcessor (KPP) is an open-source software tool used in atmospheric chemistry. Taking a set of chemical reactions and their rate coefficients as input, KPP generates Fortran 90, FORTRAN 77, C, or Matlab code of the resulting ordinary differential equations (ODEs). Solving the ODEs allows the temporal integration of the kinetic system. Efficiency is obtained by exploiting the sparsity structures of the Jacobian and of the Hessian. A comprehensive suite of stiff numerical integrators is also provided. Moreover, KPP can be used to generate the tangent linear model, as well as the continuous and discrete adjoint models of the chemical system.

ADMB or AD Model Builder is a free and open source software suite for non-linear statistical modeling. It was created by David Fournier and now being developed by the ADMB Project, a creation of the non-profit ADMB Foundation. The "AD" in AD Model Builder refers to the automatic differentiation capabilities that come from the AUTODIF Library, a C++ language extension also created by David Fournier, which implements reverse mode automatic differentiation. A related software package, ADMB-RE, provides additional support for modeling random effects.

In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with other DE, its unknown(s) consists of one function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with partial differential equations which may be with respect to more than one independent variable.
In chemistry, reaction progress kinetic analysis (RPKA) is a subset of a broad range of kinetic techniques utilized to determine the rate laws of chemical reactions and to aid in elucidation of reaction mechanisms. While the concepts guiding reaction progress kinetic analysis are not new, the process was formalized by Professor Donna Blackmond in the late 1990s and has since seen increasingly widespread use. Unlike more common pseudo-first-order analysis, in which an overwhelming excess of one or more reagents is used relative to a species of interest, RPKA probes reactions at synthetically relevant conditions Generally, this analysis involves a system in which the concentrations of multiple reactants are changing measurably over the course of the reaction. As the mechanism can vary depending on the relative and absolute concentrations of the species involved, this approach obtains results that are much more representative of reaction behavior under commonly utilized conditions than do traditional tactics. Furthermore, information obtained by observation of the reaction over time may provide insight regarding unexpected behavior such as induction periods, catalyst deactivation, or changes in mechanism.

MLAB is a multi-paradigm numerical computing environment and fourth-generation programming language was originally developed at the National Institutes of Health.

Adept is a combined automatic differentiation and array software library for the C++ programming language. The automatic differentiation capability facilitates the development of applications involving mathematical optimization. Adept is notable for having applied the template metaprogramming technique of expression templates to speed-up the differentiation of mathematical statements. Along with the efficient way that it stores the differential information, this makes it significantly faster than most other C++ tools that provide similar functionality, although comparable performance has been reported for Stan and in some cases Sacado. Differentiation may be in forward mode, reverse mode, or the full Jacobian matrix may be computed.









