
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as for , and its analytic continuation elsewhere.

In mathematics, exponentiation, denoted bn, is an operation involving two numbers: the base, b, and the exponent or power, n. When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases: In particular, .

Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:

In mathematics, Stirling's approximation is an asymptotic approximation for factorials. It is a good approximation, leading to accurate results even for small values of . It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre.

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:

In number theory, Bertrand's postulate is the theorem that for any integer , there exists at least one prime number with
In mathematics, Bertrand's postulate states that, for each , there is a prime such that . First conjectured in 1845 by Joseph Bertrand, it was first proven by Chebyshev, and a shorter but also advanced proof was given by Ramanujan.

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x) (unrelated to the number π).

Proofs of the mathematical result that the rational number 22/7 is greater than π (pi) date back to antiquity. One of these proofs, more recently developed but requiring only elementary techniques from calculus, has attracted attention in modern mathematics due to its mathematical elegance and its connections to the theory of Diophantine approximations. Stephen Lucas calls this proof "one of the more beautiful results related to approximating π". Julian Havil ends a discussion of continued fraction approximations of π with the result, describing it as "impossible to resist mentioning" in that context.

In mathematics, the polygamma function of order m is a meromorphic function on the complex numbers defined as the (m + 1)th derivative of the logarithm of the gamma function:

In mathematics, in the area of analytic number theory, the Dirichlet eta function is defined by the following Dirichlet series, which converges for any complex number having real part > 0:

In mathematics, the lemniscate constantϖ is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter, analogous to the definition of π for the circle. Equivalently, the perimeter of the lemniscate is 2ϖ. The lemniscate constant is closely related to the lemniscate elliptic functions and approximately equal to 2.62205755. It also appears in evaluation of the gamma and beta function at certain rational values. The symbol ϖ is a cursive variant of π known as variant pi represented in Unicode by the character U+03D6ϖGREEK PI SYMBOL.

In mathematics, the Dirichlet beta function is a special function, closely related to the Riemann zeta function. It is a particular Dirichlet L-function, the L-function for the alternating character of period four.
In mathematics, the Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted and is named after the mathematician Bernhard Riemann. When the argument is a real number greater than one, the zeta function satisfies the equation It can therefore provide the sum of various convergent infinite series, such as Explicit or numerically efficient formulae exist for at integer arguments, all of which have real values, including this example. This article lists these formulae, together with tables of values. It also includes derivatives and some series composed of the zeta function at integer arguments.
The gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer and half-integer arguments, but no simple expressions are known for the values at rational points in general. Other fractional arguments can be approximated through efficient infinite products, infinite series, and recurrence relations.
In number theory, Ramanujan's sum, usually denoted cq(n), is a function of two positive integer variables q and n defined by the formula

Carl Johan Malmsten was a Swedish mathematician and politician. He is notable for early research into the theory of functions of a complex variable, for the evaluation of several important logarithmic integrals and series, for his studies in the theory of Zeta-function related series and integrals, as well as for helping Mittag-Leffler start the journal Acta Mathematica. Malmsten became Docent in 1840, and then, Professor of mathematics at the Uppsala University in 1842. He was elected a member of the Royal Swedish Academy of Sciences in 1844. He was also a minister without portfolio in 1859–1866 and Governor of Skaraborg County in 1866–1879.
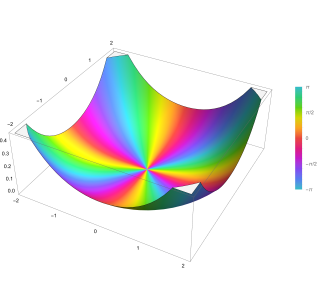
In applied mathematics, the Kelvin functions berν(x) and beiν(x) are the real and imaginary parts, respectively, of

In mathematics, the natural logarithm of 2 is the unique real number argument such that the exponential function equals two. It appears regularly in various formulas and is also given by the alternating harmonic series. The decimal value of the natural logarithm of 2 truncated at 30 decimal places is given by:
























