In number theory, a Woodall number (Wn) is any natural number of the form
for some natural number n. The first few Woodall numbers are:
Woodall numbers were first studied by Allan J. C. Cunningham and H. J. Woodall in 1917, [1] inspired by James Cullen's earlier study of the similarly defined Cullen numbers.
Woodall numbers that are also prime numbers are called Woodall primes; the first few exponents n for which the corresponding Woodall numbers Wn are prime are 2, 3, 6, 30, 75, 81, 115, 123, 249, 362, 384, ... (sequence A002234 in the OEIS ); the Woodall primes themselves begin with 7, 23, 383, 32212254719, ... (sequence A050918 in the OEIS ).
In 1976 Christopher Hooley showed that almost all Cullen numbers are composite. [2] In October 1995, Wilfred Keller published a paper discussing several new Cullen primes and the efforts made to factorise other Cullen and Woodall numbers. Included in that paper is a personal communication to Keller from Hiromi Suyama, asserting that Hooley's method can be reformulated to show that it works for any sequence of numbers n · 2n + a + b, where a and b are integers, and in particular, that almost all Woodall numbers are composite. [3] It is an open problem whether there are infinitely many Woodall primes. As of October 2018 [update] , the largest known Woodall prime is 17016602 × 217016602 − 1. [4] It has 5,122,515 digits and was found by Diego Bertolotti in March 2018 in the distributed computing project PrimeGrid. [5]
Starting with W4 = 63 and W5 = 159, every sixth Woodall number is divisible by 3; thus, in order for Wn to be prime, the index n cannot be congruent to 4 or 5 (modulo 6). Also, for a positive integer m, the Woodall number W2m may be prime only if 2m + m is prime. As of January 2019, the only known primes that are both Woodall primes and Mersenne primes are W2 = M3 = 7, and W512 = M521.
Like Cullen numbers, Woodall numbers have many divisibility properties. For example, if p is a prime number, then p divides
A generalized Woodall number base b is defined to be a number of the form n × bn − 1, where n + 2 > b; if a prime can be written in this form, it is then called a generalized Woodall prime.
The smallest value of n such that n × bn − 1 is prime for b = 1, 2, 3, ... are [6]
As of November 2021 [update] , the largest known generalized Woodall prime with base greater than 2 is 2740879 × 322740879 − 1. [7]
In mathematics, the amicable numbers are two different natural numbers related in such a way that the sum of the proper divisors of each is equal to the other number. That is, s(a)=b and s(b)=a, where s(n)=σ(n)-n is equal to the sum of positive divisors of n except n itself (see also divisor function).
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form Mn = 2n − 1 for some integer n. They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. If n is a composite number then so is 2n − 1. Therefore, an equivalent definition of the Mersenne primes is that they are the prime numbers of the form Mp = 2p − 1 for some prime p.
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
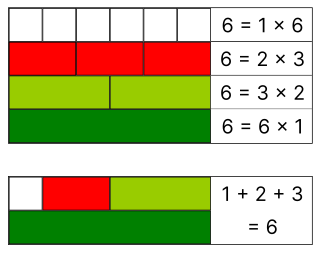
In number theory, a perfect number is a positive integer that is equal to the sum of its positive proper divisors, that is, divisors excluding the number itself. For instance, 6 has proper divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number. The next perfect number is 28, since 1 + 2 + 4 + 7 + 14 = 28.
In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. The number 2p + 1 associated with a Sophie Germain prime is called a safe prime. For example, 11 is a Sophie Germain prime and 2 × 11 + 1 = 23 is its associated safe prime. Sophie Germain primes and safe primes have applications in public key cryptography and primality testing. It has been conjectured that there are infinitely many Sophie Germain primes, but this remains unproven.
In mathematics, a Fermat number, named after Pierre de Fermat (1607–1665), the first known to have studied them, is a positive integer of the form: where n is a non-negative integer. The first few Fermat numbers are: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, ....
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for "repeated unit" and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.
In recreational mathematics, a repdigit or sometimes monodigit is a natural number composed of repeated instances of the same digit in a positional number system. The word is a portmanteau of "repeated" and "digit". Examples are 11, 666, 4444, and 999999. All repdigits are palindromic numbers and are multiples of repunits. Other well-known repdigits include the repunit primes and in particular the Mersenne primes.
In mathematics, a Cullen number is a member of the integer sequence . Cullen numbers were first studied by James Cullen in 1905. The numbers are special cases of Proth numbers.
In number theory, a k-hyperperfect number is a natural number n for which the equality holds, where σ(n) is the divisor function (i.e., the sum of all positive divisors of n). A hyperperfect number is a k-hyperperfect number for some integer k. Hyperperfect numbers generalize perfect numbers, which are 1-hyperperfect.
In number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1. Wieferich primes were first described by Arthur Wieferich in 1909 in works pertaining to Fermat's Last Theorem, at which time both of Fermat's theorems were already well known to mathematicians.
In number theory, a Wilson prime is a prime number such that divides , where "" denotes the factorial function; compare this with Wilson's theorem, which states that every prime divides . Both are named for 18th-century English mathematician John Wilson; in 1770, Edward Waring credited the theorem to Wilson, although it had been stated centuries earlier by Ibn al-Haytham.
In number theory, a regular prime is a special kind of prime number, defined by Ernst Kummer in 1850 to prove certain cases of Fermat's Last Theorem. Regular primes may be defined via the divisibility of either class numbers or of Bernoulli numbers.
23 (twenty-three) is the natural number following 22 and preceding 24.
63 (sixty-three) is the natural number following 62 and preceding 64.
In number theory, a Wagstaff prime is a prime number of the form
In mathematics, an untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer. That is, these numbers are not in the image of the aliquot sum function. Their study goes back at least to Abu Mansur al-Baghdadi, who observed that both 2 and 5 are untouchable.
A Fibonacci prime is a Fibonacci number that is prime, a type of integer sequence prime.
In number theory, a Pierpont prime is a prime number of the form for some nonnegative integers u and v. That is, they are the prime numbers p for which p − 1 is 3-smooth. They are named after the mathematician James Pierpont, who used them to characterize the regular polygons that can be constructed using conic sections. The same characterization applies to polygons that can be constructed using ruler, compass, and angle trisector, or using paper folding.
271 is the natural number after 270 and before 272.
Classes of natural numbers | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
