In number theory, an arithmetic, arithmetical, or number-theoretic function is generally any function f(n) whose domain is the positive integers and whose range is a subset of the complex numbers. Hardy & Wright include in their definition the requirement that an arithmetical function "expresses some arithmetical property of n". There is a larger class of number-theoretic functions that do not fit this definition, for example, the prime-counting functions. This article provides links to functions of both classes.
In number theory, two integers a and b are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides a does not divide b, and vice versa. This is equivalent to their greatest common divisor (GCD) being 1. One says also ais prime tob or ais coprime withb.

In number theory, a Carmichael number is a composite number which in modular arithmetic satisfies the congruence relation:

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements . It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted Fn . The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes from 1 and 2. Starting from 0 and 1, the sequence begins
In mathematics, the greatest common divisor (GCD), also known as greatest common factor (GCF), of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers x, y, the greatest common divisor of x and y is denoted . For example, the GCD of 8 and 12 is 4, that is, gcd(8, 12) = 4.
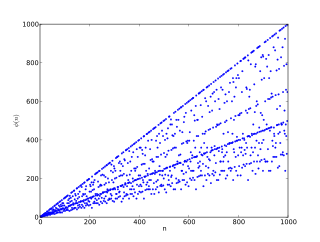
In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as or , and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.
A primality test is an algorithm for determining whether an input number is prime. Among other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not. Factorization is thought to be a computationally difficult problem, whereas primality testing is comparatively easy. Some primality tests prove that a number is prime, while others like Miller–Rabin prove that a number is composite. Therefore, the latter might more accurately be called compositeness tests instead of primality tests.
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for "repeated unit" and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.
104 is the natural number following 103 and preceding 105.
The quadratic sieve algorithm (QS) is an integer factorization algorithm and, in practice, the second-fastest method known. It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve. It is a general-purpose factorization algorithm, meaning that its running time depends solely on the size of the integer to be factored, and not on special structure or properties. It was invented by Carl Pomerance in 1981 as an improvement to Schroeppel's linear sieve.
In modular arithmetic computation, Montgomery modular multiplication, more commonly referred to as Montgomery multiplication, is a method for performing fast modular multiplication. It was introduced in 1985 by the American mathematician Peter L. Montgomery.
A divisibility rule is a shorthand and useful way of determining whether a given integer is divisible by a fixed divisor without performing the division, usually by examining its digits. Although there are divisibility tests for numbers in any radix, or base, and they are all different, this article presents rules and examples only for decimal, or base 10, numbers. Martin Gardner explained and popularized these rules in his September 1962 "Mathematical Games" column in Scientific American.
In number theory, Dixon's factorization method is a general-purpose integer factorization algorithm; it is the prototypical factor base method. Unlike for other factor base methods, its run-time bound comes with a rigorous proof that does not rely on conjectures about the smoothness properties of the values taken by a polynomial.

In number theory, a practical number or panarithmic number is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.

The Ramanujan tau function, studied by Ramanujan, is the function :\mathbb {N} \rightarrow \mathbb {Z} } defined by the following identity:
In mathematics, a Kloosterman sum is a particular kind of exponential sum. They are named for the Dutch mathematician Hendrik Kloosterman, who introduced them in 1926 when he adapted the Hardy–Littlewood circle method to tackle a problem involving positive definite diagonal quadratic forms in four variables, strengthening his 1924 dissertation research on five or more variables.
252 is the natural number following 251 and preceding 253.
In mathematics, particularly in the area of arithmetic, a modular multiplicative inverse of an integer a is an integer x such that the product ax is congruent to 1 with respect to the modulus m. In the standard notation of modular arithmetic this congruence is written as

In number theory, Berlekamp's root finding algorithm, also called the Berlekamp–Rabin algorithm, is the probabilistic method of finding roots of polynomials over the field with elements. The method was discovered by Elwyn Berlekamp in 1970 as an auxiliary to the algorithm for polynomial factorization over finite fields. The algorithm was later modified by Rabin for arbitrary finite fields in 1979. The method was also independently discovered before Berlekamp by other researchers.


















