Perfect totient number

Last updated August 02, 2022

In number theory, a perfect totient number is an integer that is equal to the sum of its iterated totients. That is, we apply the totient function to a number n, apply it again to the resulting totient, and so on, until the number 1 is reached, and add together the resulting sequence of numbers; if the sum equals n, then n is a perfect totient number.

For example, there are six positive integers less than 9 and relatively prime to it, so the totient of 9 is 6; there are two numbers less than 6 and relatively prime to it, so the totient of 6 is 2; and there is one number less than 2 and relatively prime to it, so the totient of 2 is 1; and $9 = 6 + 2 + 1$ , so 9 is a perfect totient number.

The first few perfect totient numbers are

3, 9, 15, 27, 39, 81, 111, 183, 243, 255, 327, 363, 471, 729, 2187, 2199, 3063, 4359, 4375, ... (sequence A082897 in the OEIS ).

In symbols, one writes

\varphi ^{i}(n)={\begin{cases}\varphi (n),&{\text{ if }}i=1\\\varphi (\varphi ^{i-1}(n)),&{\text{ if }}i\geq 2\end{cases}}

for the iterated totient function. Then if c is the integer such that

\displaystyle \varphi ^{c}(n)=2,

one has that n is a perfect totient number if

n=\sum _{i=1}^{c+1}\varphi ^{i}(n).

Multiples and powers of three

It can be observed that many perfect totient are multiples of 3; in fact, 4375 is the smallest perfect totient number that is not divisible by 3. All powers of 3 are perfect totient numbers, as may be seen by induction using the fact that

\displaystyle \varphi (3^{k})=\varphi (2\times 3^{k})=2\times 3^{k-1}.

Venkataraman (1975) found another family of perfect totient numbers: if $p = 4 \times 3 k + 1$ is prime, then 3p is a perfect totient number. The values of k leading to perfect totient numbers in this way are

0, 1, 2, 3, 6, 14, 15, 39, 201, 249, 1005, 1254, 1635, ... (sequence A005537 in the OEIS ).

More generally if p is a prime number greater than 3, and 3p is a perfect totient number, then p ≡ 1 (mod 4) (Mohan and Suryanarayana 1982). Not all p of this form lead to perfect totient numbers; for instance, 51 is not a perfect totient number. Iannucci et al. (2003) showed that if 9p is a perfect totient number then p is a prime of one of three specific forms listed in their paper. It is not known whether there are any perfect totient numbers of the form 3^kp where p is prime and k > 3.

Related Research Articles

In mathematics, the Fibonacci numbers, commonly denoted $F n$ , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors omit the initial terms and start the sequence from 1 and 1 or from 1 and 2. Starting from 0 and 1, the next few values in the sequence are:

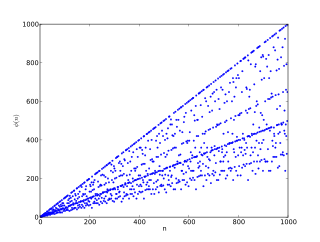
Eulers totient function Gives the number of integers relatively prime to its input

In number theory, Euler's totient function counts the positive integers up to a given integer $n$ that are relatively prime to $n$ . It is written using the Greek letter phi as $or, and may also be called Euler's phi function . In other words, it is the number of integers k in the range 1 \leq k \leq n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n .$

In modular arithmetic, a number $g$ is a primitive root modulo $n$ if every number $a$ coprime to $n$ is congruent to a power of $g$ modulo $n$ . That is, $g$ is a primitive root modulo $n$ if for every integer $a$ coprime to $n$ , there is some integer $k$ for which $g$ ^$k$ ≡ $a$ . Such a value $k$ is called the index or discrete logarithm of $a$ to the base $g$ modulo $n$ . So $g$ is a primitive root modulo $n$ if and only if $g$ is a generator of the multiplicative group of integers modulo $n$ .

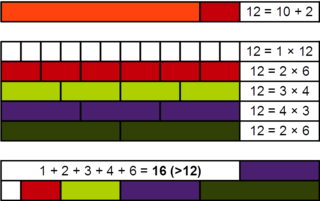
In number theory, an abundant number or excessive number is a number for which the sum of its proper divisors is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example.

In mathematics, a semiprime is a natural number that is the product of exactly two prime numbers. The two primes in the product may equal each other, so the semiprimes include the squares of prime numbers. Because there are infinitely many prime numbers, there are also infinitely many semiprimes. Semiprimes are also called biprimes.

The Lucas numbers or Lucas series are an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–1891), who studied both that sequence and the closely related Fibonacci numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences.

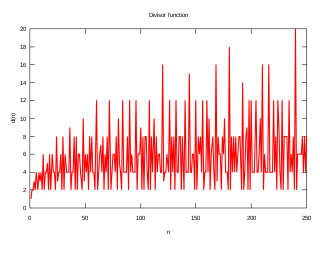
Divisor function Arithmetic function related to the divisors of an integer

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

In mathematics, and more particularly in number theory, primorial, denoted by "#", is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, the function only multiplies prime numbers.

400 is the natural number following 399 and preceding 401.

500 is the natural number following 499 and preceding 501.

In mathematics, a noncototient is a positive integer n that cannot be expressed as the difference between a positive integer m and the number of coprime integers below it. That is, m − φ(m) = n, where φ stands for Euler's totient function, has no solution for m. The cototient of n is defined as n − φ(n), so a noncototient is a number that is never a cototient.

A highly totient number $is an integer that has more solutions to the equation, where is Euler's totient function, than any integer below it. The first few highly totient numbers are$

In number theory, the nth Pisano period, written as $π$ (n), is the period with which the sequence of Fibonacci numbers taken modulo n repeats. Pisano periods are named after Leonardo Pisano, better known as Fibonacci. The existence of periodic functions in Fibonacci numbers was noted by Joseph Louis Lagrange in 1774.

Carmichael function Function in mathematical number theory

In number theory, a branch of mathematics, the Carmichael function $λ (n)$ of a positive integer $n$ is the smallest positive integer $m$ such that

In number theory, a branch of mathematics, a highly cototient number is a positive integer $which is above 1 and has more solutions to the equation$

In mathematics, a prime power is a positive integer which is a power of a single prime number. For example: $7 = 7 1$ , $9 = 3 2$ and $64 = 2 6$ are prime powers, while $6 = 2 \times 3$ , $12 = 2 2 \times 3$ and $36 = 6 2 = 2 2 \times 3 2$ are not.

A Giuga number is a composite number n such that for each of its distinct prime factors p_i we have $, or equivalently such that for each of its distinct prime factors p i we have .$

In number theory, the Dedekind psi function is the multiplicative function on the positive integers defined by

In mathematics, the Fibonacci numbers form a sequence defined recursively by:

In number theory, the totient summatory function $is a summatory function of Euler's totient function defined by:$

References

Pérez-Cacho Villaverde, Laureano (1939). "Sobre la suma de indicadores de ordenes sucesivos". Revista Matematica Hispano-Americana. 5 (3): 45–50.

Guy, Richard K. (2004). Unsolved Problems in Number Theory. New York: Springer-Verlag. p. §B41. ISBN 0-387-20860-7.

Iannucci, Douglas E.; Deng, Moujie; Cohen, Graeme L. (2003). "On perfect totient numbers" (PDF). Journal of Integer Sequences . 6 (4): 03.4.5. MR 2051959. Archived from the original (PDF) on 2017-08-12. Retrieved 2007-02-07.

Luca, Florian (2006). "On the distribution of perfect totients" (PDF). Journal of Integer Sequences. 9 (4): 06.4.4. MR 2247943 . Retrieved 2007-02-07.

Mohan, A. L.; Suryanarayana, D. (1982). "Perfect totient numbers". Number theory (Mysore, 1981). Lecture Notes in Mathematics, vol. 938, Springer-Verlag. pp. 101–105. MR 0665442.

Venkataraman, T. (1975). "Perfect totient number". The Mathematics Student . 43: 178. MR 0447089.

Hyvärinen, Tuukka (2015). "Täydelliset totienttiluvut". Tampere: Tampereen yliopisto.

This article incorporates material from Perfect Totient Number on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.