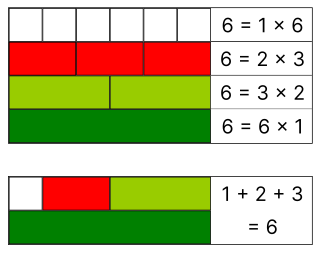
In number theory, a perfect number is a positive integer that is equal to the sum of its positive proper divisors, that is, divisors excluding the number itself. For instance, 6 has proper divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number. The next perfect number is 28, since 1 + 2 + 4 + 7 + 14 = 28.
In mathematics, a Fermat number, named after Pierre de Fermat (1607–1665), the first known to have studied them, is a positive integer of the form: where n is a non-negative integer. The first few Fermat numbers are: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, 340282366920938463463374607431768211457, ....

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.

In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid with 38 faces: 6 squares and 32 equilateral triangles. It has 60 edges and 24 vertices. Kepler first named it in Latin as cubus simus in 1619 in his Harmonices Mundi. H. S. M. Coxeter, noting it could be derived equally from the octahedron as the cube, called it snub cuboctahedron, with a vertical extended Schläfli symbol , and representing an alternation of a truncated cuboctahedron, which has Schläfli symbol .
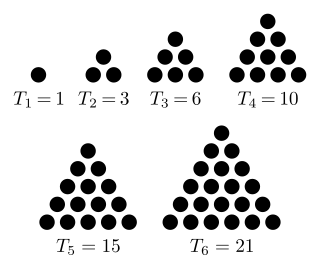
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The nth triangular number is the number of dots in the triangular arrangement with n dots on each side, and is equal to the sum of the n natural numbers from 1 to n. The sequence of triangular numbers, starting with the 0th triangular number, is
In mathematics, a polygonal number is a number that counts dots arranged in the shape of a regular polygon. These are one type of 2-dimensional figurate numbers.

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.

A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The nth pentagonal number pn is the number of distinct dots in a pattern of dots consisting of the outlines of regular pentagons with sides up to n dots, when the pentagons are overlaid so that they share one vertex. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside.

In mathematics, a heptagonal number is a figurate number that is constructed by combining heptagons with ascending size. The n-th heptagonal number is given by the formula

In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.

In elementary number theory, a centered square number is a centered figurate number that gives the number of dots in a square with a dot in the center and all other dots surrounding the center dot in successive square layers. That is, each centered square number equals the number of dots within a given city block distance of the center dot on a regular square lattice. While centered square numbers, like figurate numbers in general, have few if any direct practical applications, they are sometimes studied in recreational mathematics for their elegant geometric and arithmetic properties.
In geometry, a Heronian triangle is a triangle whose side lengths a, b, and c and area A are all positive integers. Heronian triangles are named after Heron of Alexandria, based on their relation to Heron's formula which Heron demonstrated with the example triangle of sides 13, 14, 15 and area 84.
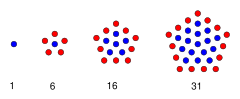
In mathematics, the centered polygonal numbers are a class of series of figurate numbers, each formed by a central dot, surrounded by polygonal layers of dots with a constant number of sides. Each side of a polygonal layer contains one more dot than each side in the previous layer; so starting from the second polygonal layer, each layer of a centered k-gonal number contains k more dots than the previous layer.
A nonagonal number, or an enneagonal number, is a figurate number that extends the concept of triangular and square numbers to the nonagon. However, unlike the triangular and square numbers, the patterns involved in the construction of nonagonal numbers are not rotationally symmetrical. Specifically, the nth nonagonal number counts the dots in a pattern of n nested nonagons, all sharing a common corner, where the ith nonagon in the pattern has sides made of i dots spaced one unit apart from each other. The nonagonal number for n is given by the formula:

A centered decagonal number is a centered figurate number that represents a decagon with a dot in the center and all other dots surrounding the center dot in successive decagonal layers. The centered decagonal number for n is given by the formula
In mathematics, a dodecagonal number is a figurate number that represents a dodecagon. The dodecagonal number for n is given by the formula
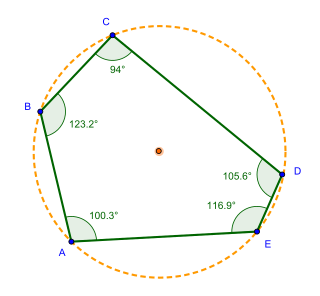
In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
In number theory, a bi-twin chain of length k + 1 is a sequence of natural numbers
A mathematical constant is a number whose value is fixed by an unambiguous definition, often referred to by a special symbol, or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as e and π occurring in such diverse contexts as geometry, number theory, statistics, and calculus.