In mathematics, an icosahedral number is a figurate number that represents an icosahedron. The nth icosahedral number is given by the formula
The first such numbers are: 1, 12, 48, 124, 255, 456, 742, 1128, 1629, 2260, 3036, 3972, 5083, … (sequence A006564 in the OEIS ).
The first study of icosahedral numbers appears to have been by René Descartes, around 1630, in his De solidorum elementis. Prior to Descartes, figurate numbers had been studied by the ancient Greeks and by Johann Faulhaber, but only for polygonal numbers, pyramidal numbers, and cubes. Descartes introduced the study of figurate numbers based on the Platonic solids and some semiregular polyhedra; his work included the icosahedral numbers. However, De solidorum elementis was lost, and not rediscovered until 1860. In the meantime, icosahedral numbers had been studied again by other mathematicians, including Friedrich Wilhelm Marpurg in 1774, Georg Simon Klügel in 1808, and Sir Frederick Pollock in 1850. [1]
In geometry, the regular icosahedron is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the skeleton of a regular icosahedron.
In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:
René Descartes was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathematics was paramount to his method of inquiry, and he connected the previously separate fields of geometry and algebra into analytic geometry. Descartes spent much of his working life in the Dutch Republic, initially serving the Dutch States Army, and later becoming a central intellectual of the Dutch Golden Age. Although he served a Protestant state and was later counted as a deist by critics, Descartes was Roman Catholic.
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions. The term can mean
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.
In mathematics, a heptagonal number is a figurate number that is constructed by combining heptagons with ascending size. The n-th heptagonal number is given by the formula
In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.
In number theory, an octahedral number is a figurate number that represents the number of spheres in an octahedron formed from close-packed spheres. The nth octahedral number can be obtained by the formula:
In geometry, the (angular) defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the Euclidean plane would. The opposite notion is the excess.
In mathematics, a centered pentagonal number is a centered figurate number that represents a pentagon with a dot in the center and all other dots surrounding the center in successive pentagonal layers. The centered pentagonal number for n is given by the formula
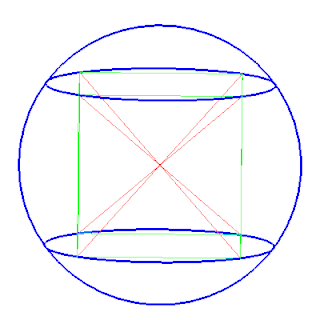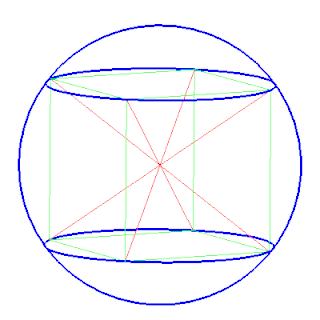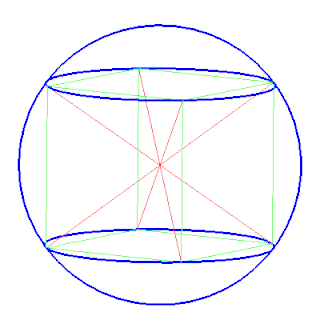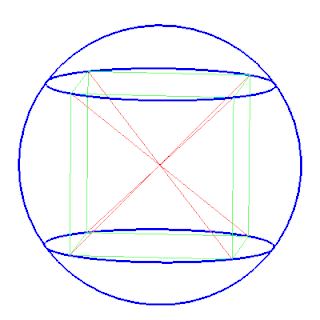
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's vertices. The word circumsphere is sometimes used to mean the same thing, by analogy with the term circumcircle. As in the case of two-dimensional circumscribed circles (circumcircles), the radius of a sphere circumscribed around a polyhedron P is called the circumradius of P, and the center point of this sphere is called the circumcenter of P.
A centered decagonal number is a centered figurate number that represents a decagon with a dot in the center and all other dots surrounding the center dot in successive decagonal layers. The centered decagonal number for n is given by the formula
In mathematics, a dodecagonal number is a figurate number that represents a dodecagon. The dodecagonal number for n is given by the formula
Pasquale ("Pat") Joseph Federico was a lifelong mathematician and longtime high-ranking official of the United States Patent Office.
In mathematics, a centered octahedral number or Haüy octahedral number is a figurate number that counts the points of a three-dimensional integer lattice that lie inside an octahedron centered at the origin. The same numbers are special cases of the Delannoy numbers, which count certain two-dimensional lattice paths. The Haüy octahedral numbers are named after René Just Haüy.
In mathematics, a centered dodecahedral number is a centered figurate number that represents a dodecahedron. The centered dodecahedral number for a specific n is given by
In mathematics, the centered icosahedral numbers also known as cuboctahedral numbers are a sequence of numbers, describing two different representations for these numbers as three-dimensional figurate numbers. As centered icosahedral numbers, they are centered numbers representing points arranged in the shape of a regular icosahedron. As cuboctahedral numbers, they represent points arranged in the shape of a cuboctahedron, and are a magic number for the face-centered cubic lattice. The centered icosahedral number for a specific is given by
In mathematics, a dodecahedral number is a figurate number that represents a dodecahedron. The nth dodecahedral number is given by the formula
Descartes on Polyhedra: A Study of the "De solidorum elementis" is a book in the history of mathematics, concerning the work of René Descartes on polyhedra. Central to the book is the disputed priority for Euler's polyhedral formula between Leonhard Euler, who published an explicit version of the formula, and Descartes, whose De solidorum elementis includes a result from which the formula is easily derived.
Classes of natural numbers | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
 | This article about a number is a stub. You can help Wikipedia by expanding it. |
