Nonagonal number

Last updated December 13, 2024

A nonagonal number, or an enneagonal number, is a figurate number that extends the concept of triangular and square numbers to the nonagon (a nine-sided polygon).^[1] However, unlike the triangular and square numbers, the patterns involved in the construction of nonagonal numbers are not rotationally symmetrical. Specifically, the nth nonagonal number counts the dots in a pattern of n nested nonagons, all sharing a common corner, where the ith nonagon in the pattern has sides made of i dots spaced one unit apart from each other. The nonagonal number for n is given by the formula:^[2]

Nonagonal numbers

The first few nonagonal numbers are:

0, 1, 9, 24, 46, 75, 111, 154, 204, 261, 325, 396, 474, 559, 651, 750, 856, 969, 1089, 1216, 1350, 1491, 1639, 1794, 1956, 2125, 2301, 2484, 2674, 2871, 3075, 3286, 3504, 3729, 3961, 4200, 4446, 4699, 4959, 5226, 5500, 5781, 6069, 6364, 6666, 6975, 7291, 7614, 7944, 8281, 8625, 8976, 9334, 9699 (sequence A001106 in the OEIS ).

The parity of nonagonal numbers follows the pattern odd-odd-even-even.

Relationship between nonagonal and triangular numbers

Letting $N_{n}$ denote the n^th nonagonal number, and using the formula $T_{n}={\frac {n(n+1)}{2}}$ for the n^th triangular number,

7N_{n}+3=T_{7n-3}

.

Test for nonagonal numbers

{\mathsf {Let}}~x={\frac {{\sqrt {56n+25}}+5}{14}}

.

If $x$ is an integer, then $n$ is the $x$ -th nonagonal number. If $x$ is not an integer, then $n$ is not nonagonal.

Related Research Articles

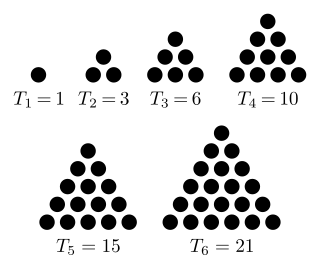
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The $n$ th triangular number is the number of dots in the triangular arrangement with $n$ dots on each side, and is equal to the sum of the $n$ natural numbers from 1 to $n$ . The sequence of triangular numbers, starting with the 0th triangular number, is

In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it equals $32$ and can be written as $3 \times 3$ .

In mathematics, a polygonal number is a number that counts dots arranged in the shape of a regular polygon. These are one type of 2-dimensional figurate numbers.

A hexagonal number is a figurate number. The nth hexagonal number h_n is the number of distinct dots in a pattern of dots consisting of the outlines of regular hexagons with sides up to n dots, when the hexagons are overlaid so that they share one vertex.

In mathematics and combinatorics, a centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice. The following figures illustrate this arrangement for the first four centered hexagonal numbers:

A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The nth pentagonal number p_n is the number of distinct dots in a pattern of dots consisting of the outlines of regular pentagons with sides up to n dots, when the pentagons are overlaid so that they share one vertex. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside.

In mathematics, a heptagonal number is a figurate number that is constructed by combining heptagons with ascending size. The n-th heptagonal number is given by the formula

A pyramidal number is the number of points in a pyramid with a polygonal base and triangular sides. The term often refers to square pyramidal numbers, which have a square base with four sides, but it can also refer to a pyramid with any number of sides. The numbers of points in the base and in layers parallel to the base are given by polygonal numbers of the given number of sides, while the numbers of points in each triangular side is given by a triangular number. It is possible to extend the pyramidal numbers to higher dimensions.

<span class="mw-page-title-main">Tetrahedral number</span> Polyhedral number representing a tetrahedron

A tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron. The $n$ th tetrahedral number, $Te n$ , is the sum of the first $n$ triangular numbers, that is,

In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.

A pronic number is a number that is the product of two consecutive integers, that is, a number of the form $. The study of these numbers dates back to Aristotle. They are also called oblong numbers, heteromecic numbers, or rectangular numbers; however, the term "rectangular number" has also been applied to the composite numbers.$

In mathematics, a star number is a centered figurate number, a centered hexagram, such as the Star of David, or the board Chinese checkers is played on.

In elementary number theory, a centered square number is a centered figurate number that gives the number of dots in a square with a dot in the center and all other dots surrounding the center dot in successive square layers. That is, each centered square number equals the number of dots within a given city block distance of the center dot on a regular square lattice. While centered square numbers, like figurate numbers in general, have few if any direct practical applications, they are sometimes studied in recreational mathematics for their elegant geometric and arithmetic properties.

In mathematics, the centered polygonal numbers are a class of series of figurate numbers, each formed by a central dot, surrounded by polygonal layers of dots with a constant number of sides. Each side of a polygonal layer contains one more dot than each side in the previous layer; so starting from the second polygonal layer, each layer of a centered k-gonal number contains k more dots than the previous layer.

In number theory, a pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1, either from left to right or from right to left. It is named because it represents the number of 3-dimensional unit spheres which can be packed into a pentatope of increasing side lengths.

A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers. The centered octagonal numbers are the same as the odd square numbers. Thus, the nth odd square number and tth centered octagonal number is given by the formula

A centered nonagonal number is a centered figurate number that represents a nonagon with a dot in the center and all other dots surrounding the center dot in successive nonagonal layers. The centered nonagonal number for n layers is given by the formula

A centered decagonal number is a centered figurate number that represents a decagon with a dot in the center and all other dots surrounding the center dot in successive decagonal layers. The centered decagonal number for n is given by the formula

204 is the natural number following 203 and preceding 205.

288 is the natural number following 287 and preceding 289. Because 288 = 2 · 12 · 12, it may also be called "two gross" or "two dozen dozen".

References

↑ Deza, Elena (2012). Figurate Numbers (1 ed.). World Scientific Publishing Co. p. 2. ISBN 978-9814355483.
↑ "A001106". Online Encyclopedia of Integer Sequences. OEIS Foundation, Inc. Retrieved 3 July 2020.

This article about a number is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Deza, Elena (2012). Figurate Numbers (1 ed.). World Scientific Publishing Co. p. 2. ISBN 978-9814355483.

[2] "A001106". Online Encyclopedia of Integer Sequences. OEIS Foundation, Inc. Retrieved 3 July 2020.

[1]

[2]

Nonagonal number

Contents