10 (ten) is the even natural number following 9 and preceding 11. Ten is the base of the decimal numeral system, the most common system of denoting numbers in both spoken and written language.
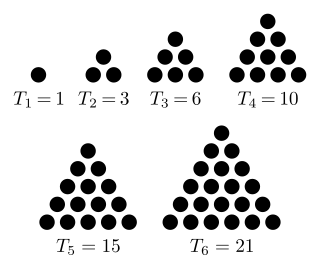
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The nth triangular number is the number of dots in the triangular arrangement with n dots on each side, and is equal to the sum of the n natural numbers from 1 to n. The sequence of triangular numbers, starting with the 0th triangular number, is

The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions. The term can mean

In mathematics and combinatorics, a centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice. The following figures illustrate this arrangement for the first four centered hexagonal numbers:

A heptagonal number is a figurate number that is constructed by combining heptagons with ascending size. The n-th heptagonal number is given by the formula
1729 is the natural number following 1728 and preceding 1730. It is the first nontrivial taxicab number, expressed as the sum of two cubic numbers in two different ways. It is also known as the Ramanujan number or Hardy–Ramanujan number, named after G. H. Hardy and Srinivasa Ramanujan.
An octagonal number is a figurate number that gives the number of points in a certain octagonal arrangement. The octagonal number for n is given by the formula 3n2 − 2n, with n > 0. The first few octagonal numbers are
126 is the natural number following 125 and preceding 127.

A centered pentagonal number is a centered figurate number that represents a pentagon with a dot in the center and all other dots surrounding the center in successive pentagonal layers. The centered pentagonal number for n is given by the formula

In elementary number theory, a centered square number is a centered figurate number that gives the number of dots in a square with a dot in the center and all other dots surrounding the center dot in successive square layers. That is, each centered square number equals the number of dots within a given city block distance of the center dot on a regular square lattice. While centered square numbers, like figurate numbers in general, have few if any direct practical applications, they are sometimes studied in recreational mathematics for their elegant geometric and arithmetic properties.

A centeredtriangular number is a centered figurate number that represents an equilateral triangle with a dot in the center and all its other dots surrounding the center in successive equilateral triangular layers.
The centered polygonal numbers are a class of series of figurate numbers, each formed by a central dot, surrounded by polygonal layers of dots with a constant number of sides. Each side of a polygonal layer contains one more dot than each side in the previous layer; so starting from the second polygonal layer, each layer of a centered k-gonal number contains k more dots than the previous layer.
A decagonal number is a figurate number that extends the concept of triangular and square numbers to the decagon. However, unlike the triangular and square numbers, the patterns involved in the construction of decagonal numbers are not rotationally symmetrical. Specifically, the nth decagonal numbers counts the dots in a pattern of n nested decagons, all sharing a common corner, where the ith decagon in the pattern has sides made of i dots spaced one unit apart from each other. The n-th decagonal number is given by the following formula
A nonagonal number, or an enneagonal number, is a figurate number that extends the concept of triangular and square numbers to the nonagon. However, unlike the triangular and square numbers, the patterns involved in the construction of nonagonal numbers are not rotationally symmetrical. Specifically, the nth nonagonal number counts the dots in a pattern of n nested nonagons, all sharing a common corner, where the ith nonagon in the pattern has sides made of i dots spaced one unit apart from each other. The nonagonal number for n is given by the formula:

A centered cube number is a centered figurate number that counts the points in a three-dimensional pattern formed by a point surrounded by concentric cubical layers of points, with i2 points on the square faces of the ith layer. Equivalently, it is the number of points in a body-centered cubic pattern within a cube that has n + 1 points along each of its edges.

In number theory, a pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1, either from left to right or from right to left. It is named because it represents the number of 3-dimensional unit spheres which can be packed into a pentatope of increasing side lengths.

A centered nonagonal number is a centered figurate number that represents a nonagon with a dot in the center and all other dots surrounding the center dot in successive nonagonal layers. The centered nonagonal number for n layers is given by the formula
A centered tetrahedral number is a centered figurate number that represents a tetrahedron. That is, it counts the dots in a three-dimensional dot pattern with a single dot surrounded by tetrahedral shells. The th centered tetrahedral number, starting at for a single dot, is:

A centered octahedral number or Haüy octahedral number is a figurate number that counts the points of a three-dimensional integer lattice that lie inside an octahedron centered at the origin. The same numbers are special cases of the Delannoy numbers, which count certain two-dimensional lattice paths. The Haüy octahedral numbers are named after René Just Haüy.
A centered dodecahedral number is a centered figurate number that represents a dodecahedron. The centered dodecahedral number for a specific n is given by















