Related Research Articles
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite collection of positive real numbers by using the product of their values. The geometric mean of numbers is the nth root of their product, i.e., for a collection of numbers a1, a2, ..., an, the geometric mean is defined as
Harmonic analysis is a branch of mathematics concerned with investigating the connections between a function and its representation in frequency. The frequency representation is found by using the Fourier transform for functions on unbounded domains such as the full real line or by Fourier series for functions on bounded domains, especially periodic functions on finite intervals. Generalizing these transforms to other domains is generally called Fourier analysis, although the term is sometimes used interchangeably with harmonic analysis. Harmonic analysis has become a vast subject with applications in areas as diverse as number theory, representation theory, signal processing, quantum mechanics, tidal analysis, spectral analysis, and neuroscience.
In mathematics, the harmonic mean is a kind of average, one of the Pythagorean means.
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose.
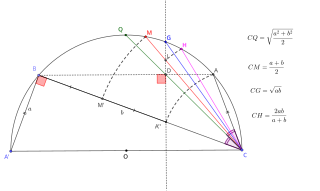
In ordinary language, an average is a single number or value that best represents a set of data. The type of average taken as most typically representative of a list of numbers is the arithmetic mean – the sum of the numbers divided by how many numbers are in the list. For example, the mean average of the numbers 2, 3, 4, 7, and 9 is 5. Depending on the context, the most representative statistic to be taken as the average might be another measure of central tendency, such as the mid-range, median, mode or geometric mean. For example, the average personal income is often given as the median – the number below which are 50% of personal incomes and above which are 50% of personal incomes – because the mean would be higher by including personal incomes from a few billionaires.
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions:
In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:
In number theory, a Wilson prime is a prime number such that divides , where "" denotes the factorial function; compare this with Wilson's theorem, which states that every prime divides . Both are named for 18th-century English mathematician John Wilson; in 1770, Edward Waring credited the theorem to Wilson, although it had been stated centuries earlier by Ibn al-Haytham.
In mathematics, a harmonic divisor number or Ore number is a positive integer whose divisors have a harmonic mean that is an integer. The first few harmonic divisor numbers are
1,000,000, or one thousand thousand, is the natural number following 999,999 and preceding 1,000,001. The word is derived from the early Italian millione, from mille, "thousand", plus the augmentative suffix -one.
In mathematics, Wolstenholme's theorem states that for a prime number , the congruence
100,000 (one hundred thousand) is the natural number following 99,999 and preceding 100,001. In scientific notation, it is written as 105.
149 is the natural number between 148 and 150.
In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the unsigned Stirling numbers of the first kind count permutations according to their number of cycles.
Regular numbers are numbers that evenly divide powers of 60 (or, equivalently, powers of 30). Equivalently, they are the numbers whose only prime divisors are 2, 3, and 5. As an example, 602 = 3600 = 48 × 75, so as divisors of a power of 60 both 48 and 75 are regular.
205 is the natural number following 204 and preceding 206.
In number theory, a Wolstenholme prime is a special type of prime number satisfying a stronger version of Wolstenholme's theorem. Wolstenholme's theorem is a congruence relation satisfied by all prime numbers greater than 3. Wolstenholme primes are named after mathematician Joseph Wolstenholme, who first described this theorem in the 19th century.
References
Classes of natural numbers | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
 | This article about a number is a stub. You can help Wikipedia by expanding it. |