In mathematics, the Bernoulli numbersBn are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.

In mathematics, the gamma function is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function is defined for all complex numbers except non-positive integers, and for every positive integer , The gamma function can be defined via a convergent improper integral for complex numbers with positive real part:

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as for , and its analytic continuation elsewhere.

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 32. The smallest positive square-free numbers are

Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The original such product was given for the sum of all positive integers raised to a certain power as proven by Leonhard Euler. This series and its continuation to the entire complex plane would later become known as the Riemann zeta function.

In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0, −1, −2, … by

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.
In number theory, Khinchin's constant is a mathematical constant related to the simple continued fraction expansions of many real numbers. In particular Aleksandr Yakovlevich Khinchin proved that for almost all real numbers x, the coefficients ai of the continued fraction expansion of x have a finite geometric mean that is independent of the value of x. It is known as Khinchin's constant and denoted by K0.

In number theory, the Mertens function is defined for all positive integers n as

In mathematics, in the area of analytic number theory, the Dirichlet eta function is defined by the following Dirichlet series, which converges for any complex number having real part > 0:
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
In mathematics, Apéry's theorem is a result in number theory that states the Apéry's constant ζ(3) is irrational. That is, the number
In mathematics, a rational zeta series is the representation of an arbitrary real number in terms of a series consisting of rational numbers and the Riemann zeta function or the Hurwitz zeta function. Specifically, given a real number x, the rational zeta series for x is given by
In mathematics, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number
In mathematics, the Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted and is named after the mathematician Bernhard Riemann. When the argument is a real number greater than one, the zeta function satisfies the equation It can therefore provide the sum of various convergent infinite series, such as Explicit or numerically efficient formulae exist for at integer arguments, all of which have real values, including this example. This article lists these formulae, together with tables of values. It also includes derivatives and some series composed of the zeta function at integer arguments.
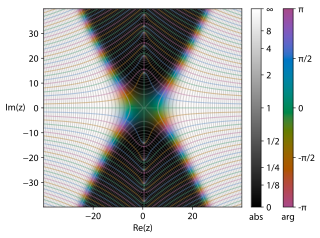
In mathematics, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation. The function is named in honour of Bernhard Riemann.
In mathematics, a natural number a is a unitary divisor of a number b if a is a divisor of b and if a and are coprime, having no common factor other than 1. Equivalently, a divisor a of b is a unitary divisor if and only if every prime factor of a has the same multiplicity in a as it has in b.

In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann, after whom it is named.
In mathematics, the Riemann–Siegel formula is an asymptotic formula for the error of the approximate functional equation of the Riemann zeta function, an approximation of the zeta function by a sum of two finite Dirichlet series. It was found by Siegel (1932) in unpublished manuscripts of Bernhard Riemann dating from the 1850s. Siegel derived it from the Riemann–Siegel integral formula, an expression for the zeta function involving contour integrals. It is often used to compute values of the Riemann–Siegel formula, sometimes in combination with the Odlyzko–Schönhage algorithm which speeds it up considerably. When used along the critical line, it is often useful to use it in a form where it becomes a formula for the Z function.













