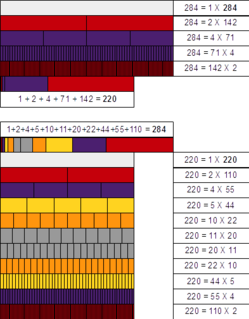
Amicable numbers are two different natural numbers related in such a way that the sum of the proper divisors of each is equal to the other number. That is, σ(a)=b+a and σ(b)=a+b, where σ(n) is equal to the sum of positive divisors of n.

In mathematics, a divisor of an integer, also called a factor of , is an integer that may be multiplied by some integer to produce . In this case, one also says that is a multiple of An integer is divisible or evenly divisible by another integer if is a divisor of ; this implies dividing by leaves no remainder.
A highly composite number is a positive integer with more divisors than any smaller positive integer has. The related concept of largely composite number refers to a positive integer which has at least as many divisors as any smaller positive integer. The name can be somewhat misleading, as two highly composite numbers are not actually composite numbers.

In mathematics, a multiply perfect number is a generalization of a perfect number.
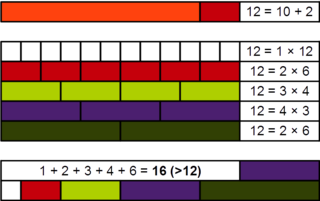
In number theory, an abundant number or excessive number is a number for which the sum of its proper divisors is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example.

In number theory, a deficient number or defective number is a number n for which the sum of divisors of n is less than 2n. Equivalently, it is a number for which the sum of proper divisors is less than n. For example, the proper divisors of 8 are 1, 2, and 4, and their sum is less than 8, so 8 is deficient.
In mathematics, a quasiperfect number is a natural number n for which the sum of all its divisors is equal to 2n + 1. Equivalently, n is the sum of its non-trivial divisors. No quasiperfect numbers have been found so far.

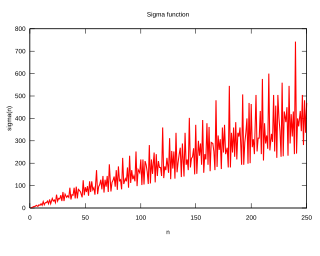
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

120, read as one hundred [and] twenty, is the natural number following 119 and preceding 121.
An untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer. That is, these numbers are not in the image of the aliquot sum function. Their study goes back at least to Abu Mansur al-Baghdadi, who observed that both 2 and 5 are untouchable.

In number theory, a practical number or panarithmic number is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.
5040 is a factorial (7!), a superior highly composite number, abundant number, colossally abundant number and the number of permutations of 4 items out of 10 choices. It is also one less than a square, making a Brown number pair.
In mathematics, a superabundant number is a certain kind of natural number. A natural number n is called superabundant precisely when, for all m < n
In mathematics, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Formally, a number n is said to be colossally abundant if there is an ε > 0 such that for all k > 1,
225 is the natural number following 224 and preceding 226.
In number theory, friendly numbers are two or more natural numbers with a common abundancy index, the ratio between the sum of divisors of a number and the number itself. Two numbers with the same "abundancy" form a friendly pair; n numbers with the same "abundancy" form a friendly n-tuple.
288 is the natural number following 287 and preceding 289. Because 288 = 2 · 12 · 12, it may also be called "two gross" or "two dozen dozen".
Leonidas (Leon) Alaoglu was a mathematician, known for his result, called Alaoglu's theorem on the weak-star compactness of the closed unit ball in the dual of a normed space, also known as the Banach–Alaoglu theorem.
In number theory, the aliquot sums(n) of a positive integer n is the sum of all proper divisors of n, that is, all divisors of n other than n itself. That is,
840 is the natural number following 839 and preceding 841.












