
Johann Carl Friedrich Gauss was a German mathematician, geodesist, and physicist who made significant contributions to many fields in mathematics and science. Gauss ranks among history's most influential mathematicians. He is referred to as the "Prince of Mathematicians".

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

Extraterrestrial life or alien life is life which does not originate from Earth. No extraterrestrial life has yet been conclusively detected. Such life might range from simple forms such as prokaryotes to intelligent beings, possibly bringing forth civilizations that might be far more advanced than humanity. The Drake equation speculates about the existence of sapient life elsewhere in the universe. The science of extraterrestrial life is known as astrobiology.

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).
Eudoxus of Cnidus was an ancient Greek astronomer, mathematician, doctor, and lawmaker. He was a student of Archytas and Plato. All of his original works are lost, though some fragments are preserved in Hipparchus' Commentaries on the Phenomena of Aratus and Eudoxus. Spherics by Theodosius of Bithynia may be based on a work by Eudoxus.

The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 2nd century CE. This book is one of the earliest surviving mathematical texts from China, the first being the Suan shu shu and Zhoubi Suanjing. It lays out an approach to mathematics that centres on finding the most general methods of solving problems, which may be contrasted with the approach common to ancient Greek mathematicians, who tended to deduce propositions from an initial set of axioms.

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. It is a circular arc that measures 180°. It has only one line of symmetry.

In geometry, the statement that the angles opposite the equal sides of an isosceles triangle are themselves equal is known as the pons asinorum, typically translated as "bridge of asses". This statement is Proposition 5 of Book 1 in Euclid's Elements, and is also known as the isosceles triangle theorem. Its converse is also true: if two angles of a triangle are equal, then the sides opposite them are also equal. The term is also applied to the Pythagorean theorem.

The communication with extraterrestrial intelligence (CETI) is a branch of the search for extraterrestrial intelligence (SETI) that focuses on composing and deciphering interstellar messages that theoretically could be understood by another technological civilization. The best-known CETI experiment of its kind was the 1974 Arecibo message composed by Frank Drake.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.

Hippocrates of Chios was an ancient Greek mathematician, geometer, and astronomer.

Ancient Greek astronomy is the astronomy written in the Greek language during classical antiquity. Greek astronomy is understood to include the Ancient Greek, Hellenistic, Greco-Roman, and late antique eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the language of scholarship throughout the Hellenistic world following the conquests of Alexander. This phase of Greek astronomy is also known as Hellenistic astronomy, while the pre-Hellenistic phase is known as Classical Greek astronomy. During the Hellenistic and Roman periods, many of the Greek and non-Greek astronomers working in the Greek tradition studied at the Museum and the Library of Alexandria in Ptolemaic Egypt.

Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata, who discovered the sine function. During the Middle Ages, the study of trigonometry continued in Islamic mathematics, by mathematicians such as Al-Khwarizmi and Abu al-Wafa. It became an independent discipline in the Islamic world, where all six trigonometric functions were known. Translations of Arabic and Greek texts led to trigonometry being adopted as a subject in the Latin West beginning in the Renaissance with Regiomontanus. The development of modern trigonometry shifted during the western Age of Enlightenment, beginning with 17th-century mathematics and reaching its modern form with Leonhard Euler (1748).
This is a timeline of mathematicians in ancient Greece.
The following is a timeline of key developments of geometry:

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
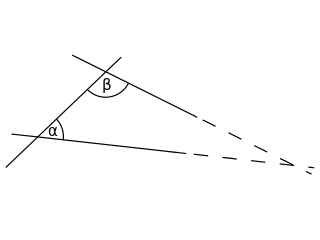
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.
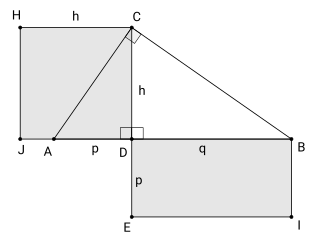
In Euclidean geometry, the right triangle altitude theorem or geometric mean theorem is a relation between the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude.


















