The derivative of a function of a real variable measures the sensitivity to change of the function value with respect to a change in its argument. Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.

In mathematics, an exponential function is a function of the form

In mathematics, a linear equation is an equation that may be put in the form

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f (x) at a point x = c on the curve if the line passes through the point (c, f ) on the curve and has slope f'(c) where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
In physics, angular velocity refers to how fast an object rotates or revolves relative to another point, i.e. how fast the angular position or orientation of an object changes with time. There are two types of angular velocity: orbital angular velocity and spin angular velocity. Spin angular velocity refers to how fast a rigid body rotates with respect to its centre of rotation. Orbital angular velocity refers to how fast a rigid body's centre of rotation revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. In general, angular velocity is measured in angle per unit time, radians per second in SI units, and is usually represented by the symbol omega. By convention, positive angular velocity indicates counter-clockwise rotation, while negative is clockwise.

A logistic function or logistic curve is a common "S" shape, with equation:

The moment of inertia, otherwise known as the angular mass or rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis; similar to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rotation rate. It is an extensive (additive) property: for a point mass the moment of inertia is just the mass times the square of the perpendicular distance to the rotation axis. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems. Its simplest definition is the second moment of mass with respect to distance from an axis. For bodies constrained to rotate in a plane, only their moment of inertia about an axis perpendicular to the plane, a scalar value, matters. For bodies free to rotate in three dimensions, their moments can be described by a symmetric 3 × 3 matrix, with a set of mutually perpendicular principal axes for which this matrix is diagonal and torques around the axes act independently of each other.
In physics, Wick rotation, named after Gian Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable. This transformation is also used to find solutions to problems in quantum mechanics and other areas.
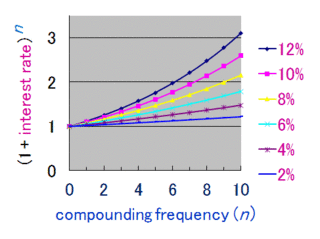
Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, interest on interest. It is the result of reinvesting interest, rather than paying it out, so that interest in the next period is then earned on the principal sum plus previously accumulated interest. Compound interest is standard in finance and economics.
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:

In finance, the duration of a financial asset that consists of fixed cash flows, for example a bond, is the weighted average of the times until those fixed cash flows are received. When the price of an asset is considered as a function of yield, duration also measures the price sensitivity to yield, the rate of change of price with respect to yield or the percentage change in price for a parallel shift in yields.

The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor.

In science and engineering, a log–log graph or log–log plot is a two-dimensional graph of numerical data that uses logarithmic scales on both the horizontal and vertical axes. Monomials – relationships of the form – appear as straight lines in a log–log graph, with the power term corresponding to the slope, and the constant term corresponding to the intercept of the line. Thus these graphs are very useful for recognizing these relationships and estimating parameters. Any base can be used for the logarithm, though most common are 10, e, and 2.

In calculus, the second derivative, or the second order derivative, of a function f is the derivative of the derivative of f. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is the instantaneous acceleration of the vehicle, or the rate at which the velocity of the vehicle is changing with respect to time. In Leibniz notation:

The Gompertz curve or Gompertz function, is a type of mathematical model for a time series and is named after Benjamin Gompertz (1779-1865). It is a sigmoid function which describes growth as being slowest at the start and end of a given time period. The right-hand or future value asymptote of the function is approached much more gradually by the curve than the left-hand or lower valued asymptote. This is in contrast to the simple logistic function in which both asymptotes are approached by the curve symmetrically. It is a special case of the generalised logistic function. The function was originally designed to describe human mortality, but since has been modified to be applied in biology, with regards to detailing populations.

The optical transfer function (OTF) of an optical system such as a camera, microscope, human eye, or projector specifies how different spatial frequencies are handled by the system. It is used by optical engineers to describe how the optics project light from the object or scene onto a photographic film, detector array, retina, screen, or simply the next item in the optical transmission chain. A variant, the modulation transfer function (MTF), neglects phase effects, but is equivalent to the OTF in many situations.
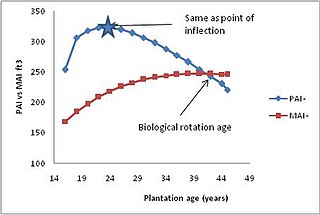
In forestry, the optimal rotation age is the growth period required to derive maximum value from a stand of timber. The calculation of this period is specific to each stand and to the economic and sustainability goals of the harvester.

Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.