Polygram (geometry)

For the Dutch record label, see PolyGram.

Regular polygrams {n/d}, with red lines showing constant d, and blue lines showing compound sequences k{n/d}

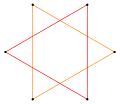
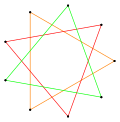
In geometry, a generalized polygon can be called a polygram, and named specifically by its number of sides. All polygons are polygrams, but they can also include disconnected sets of edges, called a compound polygon. For example, a regular pentagram, {5/2}, has 5 sides, and the regular hexagram, {6/2} or 2{3}, has 6 sides divided into two triangles.

A regular polygram {p/q} can either be in a set of regular star polygons (for gcd(p,q) = 1, q > 1) or in a set of regular polygon compounds (if gcd(p,q) > 1). ^[1]

Etymology

The polygram names combine a numeral prefix, such as penta- , with the Greek suffix -gram (in this case generating the word pentagram ). The prefix is normally a Greek cardinal, but synonyms using other prefixes exist. The -gram suffix derives from γραμμῆς (grammos) meaning a line. ^[2]

Generalized regular polygons

Further information: Regular polygon § Regular star polygons

A regular polygram, as a general regular polygon, is denoted by its Schläfli symbol {p/q}, where p and q are relatively prime (they share no factors) and q ≥ 2. For integers p and q, it can be considered as being constructed by connecting every qth point out of p points regularly spaced in a circular placement. ^{[3] [1]}

{5/2}

{7/2}

{7/3}

{8/3}

{9/2}

{9/4}

{10/3}...

Regular compound polygons

Further information: List of regular polytopes and compounds § Two dimensions

In other cases where n and m have a common factor, a polygram is interpreted as a lower polygon, {n/k, m/k}, with k = gcd(n,m), and rotated copies are combined as a compound polygon. These figures are called regular compound polygons.

Some regular polygon compounds

Triangles...			Squares...		Pentagons...	Pentagrams...
{6/2}=2{3}	{9/3}=3{3}	{12/4}=4{3}	{8/2}=2{4}	{12/3}=3{4}	{10/2}=2{5}	{10/4}=2{5/2}	{15/6}=3{5/2}

See also

• List of regular polytopes and compounds § Stars

References

1. Weisstein, Eric W. "Polygram". MathWorld .
2. γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
3. Coxeter, Harold Scott Macdonald (1973). Regular polytopes . Courier Dover Publications. p.  93. ISBN   978-0-486-61480-9.

• Cromwell, P.; Polyhedra, CUP, Hbk. 1997, ISBN   0-521-66432-2. Pbk. (1999), ISBN   0-521-66405-5. p. 175
• Grünbaum, B. and G.C. Shephard; Tilings and patterns , New York: W. H. Freeman & Co., (1987), ISBN   0-7167-1193-1.
• Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN   978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)
• Robert Lachlan, An Elementary Treatise on Modern Pure Geometry. London: Macmillan, 1893, p. 83 polygrams.
• Branko Grünbaum, Metamorphoses of polygons, published in The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994)